Cálculo com múltiplas variáveis

Formulando as definições para campos vetoriais, estas também sendo válidas para campos escalares. Seja

${\displaystyle \mathbf {f} :V\longrightarrow W}$

um campo vetorial que faz corresponder a todo ponto P definido biunivocamente por sua vetor posição um vetor ${\displaystyle \mathbf {f} {\big (}\mathbf {OP} {\big )}}$ onde o ponto O é a origem de coordenadas.

${\displaystyle V\subseteq \mathbb {R} ^{n},W\subseteq \mathbb {R} ^{m},}$ com ${\displaystyle n>1}$ e ${\displaystyle m\geqslant 1}$. Quando ${\displaystyle m=1}$ temos um campo escalar. Para ${\displaystyle m>1}$ temos um campo vetorial. Utiliza-se a norma euclidiana para encontrar a magnitude dos vetores.

Sejam ${\displaystyle \mathbf {a} \in \mathbb {R} ^{n}}$ e ${\displaystyle \mathbf {b} \in \mathbb {R} ^{m}.}$ Escrevemos:

${\displaystyle \lim _{\mathbf {x} \to \mathbf {a} }\mathbf {f} {\big (}\mathbf {x} {\big )}=\mathbf {b} }$,

ou ainda,

${\displaystyle \mathbf {f} (\mathbf {x} )\rightarrow \mathbf {b} }$ cuando ${\displaystyle \mathbf {x} \rightarrow \mathbf {a} }$

para expressar o seguinte:

${\displaystyle \lim _{{\big \|}\mathbf {x-a} {\big \|}\to 0}{\big \|}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\big \|}=0}$

onde ${\displaystyle {\big \|}\mathbf {x} {\big \|}}$ é a norma euclideana de ${\displaystyle \mathbf {x} }$.

Expresando-o em função das componentes de ${\displaystyle \mathbf {x} ={\big (}x_{1},\ldots ,x_{n}{\big )},\mathbf {a} ={\big (}a_{1},\ldots ,a_{n}{\big )},}$

${\displaystyle \lim _{{\big (}x_{1},\ldots ,x_{n}{\big )}\to {\big (}a_{1},\ldots ,a_{n}{\big )}}\mathbf {f} {\big (}x_{1},\ldots ,x_{n}{\big )}=\mathbf {b} }$

ou, de forma equivalente,

${\displaystyle \lim _{\mathbf {x} \to \mathbf {a} }\mathbf {f} {\big (}\mathbf {x} {\big )}=\mathbf {b} }$

Dizemos que uma função ${\displaystyle \mathbf {f} }$ é contínua em ${\displaystyle \mathbf {a} \Leftrightarrow \lim _{\mathbf {x} \to \mathbf {a} }\mathbf {f} {\big (}\mathbf {x} {\big )}=\mathbf {f} {\big (}\mathbf {a} {\big )}}$.

${\displaystyle \lim _{\mathbf {x} \to \mathbf {a} }\mathbf {f} {\big (}\mathbf {x} {\big )}=\mathbf {b} ,\lim _{\mathbf {x} \to \mathbf {a} }\mathbf {g} {\big (}\mathbf {x} {\big )}=\mathbf {c} \Rightarrow }$

a) ${\displaystyle \lim _{\mathbf {x} \to \mathbf {a} }{\big [}\mathbf {f} +\mathbf {g} {\big ]}{\big (}\mathbf {x} {\big )}=\mathbf {b} +\mathbf {c} }$

b) ${\displaystyle \lim _{\mathbf {x} \to \mathbf {a} }\lambda \mathbf {f} {\big (}\mathbf {x} {\big )}=\lambda \mathbf {b} \quad \forall \lambda \in \mathbb {R} }$

c) ${\displaystyle \lim _{\mathbf {x} \to \mathbf {a} }{\big (}\mathbf {f} \cdot \mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}=\mathbf {b} \cdot \mathbf {c} }$

(produto escalar de ${\displaystyle \mathbf {b} }$ com ${\displaystyle \mathbf {c} }$).

d) ${\displaystyle \lim _{\mathbf {x} \to \mathbf {a} }{\Big \|}\mathbf {f} {\big (}\mathbf {x} {\big )}{\Big \|}={\big \|}\mathbf {b} {\big \|}}$

Sabemos que a) e b) no teorema se verificam se ${\displaystyle f}$ e ${\displaystyle g}$ são funções escalares. Portanto, se

${\displaystyle \mathbf {b} ={\big (}b_{1},\ldots ,b_{m}{\big )},\mathbf {c} ={\big (}c_{1},\ldots ,c_{m}{\big )}}$ temos

${\displaystyle {\begin{array}{rl}a)&\mathbf {f} {\big (}\mathbf {x} )={\big [}f_{1}{\big (}\mathbf {x} {\big )},\ldots ,f_{m}{\big (}\mathbf {x} {\big )}{\big ]},\mathbf {g} {\big (}\mathbf {x} )={\Big [}g_{1}{\big (}\mathbf {x} {\big )},\ldots ,g_{m}{\big (}\mathbf {x} {\big )}{\Big ]}\\&\lim _{\mathbf {x} \to \mathbf {a} }{\big (}\mathbf {f} +\mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}=\lim _{\mathbf {x} \to \mathbf {a} }{\Big [}{\big (}f_{1}+g_{1}{\big )}{\big (}\mathbf {x} {\big )},\ldots ,{\big (}f_{m}+g_{m}{\big )}{\big (}\mathbf {x} {\big )}{\Big ]}=\\&{\Big [}\lim _{\mathbf {x} \to \mathbf {a} }{\big (}f_{1}+g_{1}{\big )}{\big (}\mathbf {x} {\big )},\ldots ,\lim _{\mathbf {x} \to \mathbf {a} }{\big (}f_{m}+g_{m}{\big )}{\big (}\mathbf {x} {\big )}{\Big ]}=\\&{\Big [}\lim _{\mathbf {x} \to \mathbf {a} }f_{1}{\big (}\mathbf {x} {\big )}+\lim _{\mathbf {x} \to \mathbf {a} }g_{1}(\mathbf {x} {\big )},\ldots ,\lim _{\mathbf {x} \to \mathbf {a} }f_{m}{\big (}\mathbf {x} {\big )}+\lim _{\mathbf {x} \to \mathbf {a} }g_{m}{\big (}\mathbf {x} {\big )}{\Big ]}=\\&{\big (}b_{1}+c_{1},\ldots ,b_{m}+c_{m}{\big )}={\big (}b_{1},\ldots ,b_{m}{\big )}+{\big (}c_{1},\ldots ,c_{m}{\big )}=\mathbf {b} +\mathbf {c} \end{array}}}$

${\displaystyle {\begin{array}{rl}b)&\lim _{\mathbf {x} \to \mathbf {a} }\lambda \mathbf {f} {\big (}\mathbf {x} {\big )}=\lim _{\mathbf {x} \to \mathbf {a} }\lambda {\Big [}f_{1}{\big (}\mathbf {x} {\big )},\ldots ,f_{m}{\big (}\mathbf {x} {\big )}{\Big ]}=\lim _{\mathbf {x} \to \mathbf {a} }{\Big [}\lambda f_{1}{\big (}\mathbf {x} {\big )},\ldots ,\lambda f_{m}{\big (}\mathbf {x} {\big )}{\Big ]}=\\&{\Big [}\lim _{\mathbf {x} \to \mathbf {a} }\lambda f_{1}{\big (}\mathbf {x} {\big )},\ldots ,\lim _{\mathbf {x} \to \mathbf {a} }\lambda f_{m}{\big (}\mathbf {x} {\big )}{\Big ]}={\Big [}\lambda \lim _{\mathbf {x} \to \mathbf {a} }f_{1}{\big (}\mathbf {x} {\big )},\ldots ,\lambda \lim _{\mathbf {x} \to \mathbf {a} }f_{m}{\big (}\mathbf {x} {\big )}{\Big ]}=\\&\lambda {\Big [}\lim _{\mathbf {x} \to \mathbf {a} }f_{1}{\big (}\mathbf {x} {\big )},\ldots ,\lim _{\mathbf {x} \to \mathbf {a} }f_{m}{\big (}\mathbf {x} {\big )}{\Big ]}=\lambda {\big (}b_{1},\ldots ,b_{m}{\big )}=\lambda \mathbf {b} \end{array}}}$

${\displaystyle c)\quad {\big (}\mathbf {f} \cdot \mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}-\mathbf {b} \cdot \mathbf {c} ={\Big [}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\Big ]}\cdot {\Big [}\mathbf {g} {\big (}\mathbf {x} {\big )}-\mathbf {c} {\Big ]}+\mathbf {b} \cdot {\Big [}\mathbf {g} {\big (}\mathbf {x} {\big )}-\mathbf {c} {\Big ]}+\mathbf {c} \cdot {\Big [}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\Big ]}}$

Aplicando a desigualdade triangular e a desigualdade de Cauchy-Schwarz temos

${\displaystyle {\begin{array}{l}{\Big |}{\big (}\mathbf {f} \cdot \mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}-\mathbf {b} \cdot \mathbf {c} {\Big |}\leqslant {\Big \|}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\Big \|}\cdot {\Big \|}\mathbf {g} {\big (}\mathbf {x} {\big )}-\mathbf {c} {\Big \|}+{\big \|}\mathbf {b} {\big \|}\cdot {\Big \|}\mathbf {g} {\big (}\mathbf {x} {\big )}-\mathbf {c} {\Big \|}+{\big \|}\mathbf {c} {\big \|}\cdot {\Big \|}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\Big \|}\Rightarrow \\0\leqslant \lim _{{\big \|}\mathbf {x} -\mathbf {a} {\big \|}\to 0}{\Big |}{\big (}\mathbf {f} \cdot \mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}-\mathbf {b} \cdot \mathbf {c} {\Big |}\leqslant \lim _{{\big \|}\mathbf {x} -\mathbf {a} {\big \|}\to 0}{\Big \|}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\Big \|}\cdot \lim _{{\big \|}\mathbf {x} -\mathbf {a} {\big \|}\to 0}{\Big \|}\mathbf {g} {\big (}\mathbf {x} {\big )}-\mathbf {c} {\Big \|}+\\{\big \|}\mathbf {b} {\big \|}\cdot \lim _{{\big \|}\mathbf {x} -\mathbf {a} {\big \|}\to 0}{\Big \|}\mathbf {g} {\big (}\mathbf {x} {\big )}-\mathbf {c} {\Big \|}+{\big \|}\mathbf {c} {\big \|}\lim _{{\big \|}\mathbf {x} -\mathbf {a} {\big \|}\to 0}{\Big \|}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\Big \|}=0\cdot 0+{\big \|}\mathbf {b} {\big \|}\cdot 0+{\big \|}\mathbf {c} {\big \|}\cdot 0=\\0\end{array}}}$

, como queríamos demonstrar.

${\displaystyle d)\quad \mathbf {g} {\big (}\mathbf {x} {\big )}=\mathbf {f} {\big (}\mathbf {x} {\big )},\mathbf {c} =\mathbf {b} \Rightarrow \lim _{\mathbf {x} \to \mathbf {a} }{\Big \|}\mathbf {f} {\big (}\mathbf {x} {\big )}{\Big \|}^{2}={\big \|}\mathbf {b} {\big \|}^{2}}$, como queríamos demonstrar.

Sejam ${\displaystyle \mathbf {f} }$ e ${\displaystyle \mathbf {g} }$ duas funções tais que a função composta ${\displaystyle \mathbf {f} \circ \mathbf {g} }$ está definida em ${\displaystyle \mathbf {a} }$, sendo

${\displaystyle {\big (}\mathbf {f} \circ \mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}=\mathbf {f} {\Big [}\mathbf {g} {\big (}\mathbf {x} {\big )}{\Big ]}}$

${\displaystyle \mathbf {g} }$ é contínua em ${\displaystyle \mathbf {a} }$ e ${\displaystyle \mathbf {f} }$ é contínua em ${\displaystyle \mathbf {g} {\big (}\mathbf {a} {\big )}\Rightarrow {\big (}\mathbf {f} \circ \mathbf {g} {\big )}}$ é contínua em ${\displaystyle \mathbf {a} }$.

Sejam ${\displaystyle \mathbf {y} =\mathbf {g} {\big (}\mathbf {x} {\big )}}$ e ${\displaystyle \mathbf {b} =\mathbf {g} {\big (}\mathbf {a} {\big )}}$. Então,

${\displaystyle {\begin{array}{l}\lim _{{\big \|}\mathbf {x} -\mathbf {a} {\big \|}\to 0}{\Big \|}\mathbf {f} {\Big [}\mathbf {g} {\big (}\mathbf {x} {\big )}{\Big ]}-\mathbf {f} {\Big [}\mathbf {g} {\big (}\mathbf {a} {\big )}{\Big ]}{\Big \|}=\lim _{{\big \|}\mathbf {y} -\mathbf {b} {\big \|}\to 0}{\Big \|}\mathbf {f} {\big (}\mathbf {y} {\big )}-\mathbf {f} {\big (}\mathbf {b} {\big )}{\Big \|}=0\Rightarrow \\\lim _{\mathbf {x} \to \mathbf {a} }\mathbf {f} {\Big [}\mathbf {g} {\big (}\mathbf {x} {\big )}{\Big ]}=\mathbf {f} {\Big [}\mathbf {g} {\big (}\mathbf {a} {\big )}{\Big ]}\end{array}}}$

como queríamos demostrar.

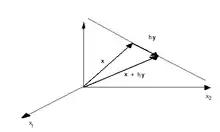
Seja ${\displaystyle f:S\subseteq \mathbb {R} ^{n}\longrightarrow \mathbb {R} }$. Seja ${\displaystyle \mathbf {x} }$ um vetor cuja origem é a origem das coordenadas e cujo extremo ${\displaystyle \in S,}$ e ${\displaystyle \mathbf {y} }$ um vetor arbitrário de ${\displaystyle \mathbb {R} ^{n}}$. Definimos a derivada de f em ${\displaystyle \mathbf {x} }$ em relação a ${\displaystyle \mathbf {y} }$ como

${\displaystyle f'{\big (}\mathbf {x}$ ;\mathbf {y} {\big )}=\lim _{h\to 0}{\cfrac {f{\big (}\mathbf {x} +h\mathbf {y} {\big )}-f{\big (}\mathbf {x} {\big )}}{h}}}

${\displaystyle {\cfrac {\partial f}{\partial x_{k}}}=\lim _{h\to 0}{\cfrac {f{\big (}x_{1},\ldots ,x_{k}+h,\ldots ,x_{n}{\big )}-f{\big (}x_{1},\ldots ,x_{k},\ldots ,x_{n}{\big )}}{h}}}$

Se derivamos a expressão anterior em relação a uma segunda variável, ${\displaystyle x_{j}}$, teremos ${\displaystyle {\cfrac {\partial ^{2}f}{\partial x_{j}\partial x_{k}}}}$. Na prática, calcularemos ${\displaystyle {\cfrac {\partial f}{\partial x_{k}}}}$ derivando em relação a ${\displaystyle x_{k}}$ e supondo ${\displaystyle x_{j},\quad \forall j\neq k}$ constante.

Dizemos que f é diferenciável em ${\displaystyle \mathbf {a} \Leftrightarrow }$

${\displaystyle \exists f_{L}:\mathbb {R} ^{n}\longrightarrow \mathbb {R} {\Big |}\lim _{{\big \|}\mathbf {v} {\big \|}\to \mathbf {0} }f{\big (}\mathbf {a} +\mathbf {v} {\big )}=f{\big (}\mathbf {a} {\big )}+f_{L}{\big (}\mathbf {v} {\big )}}$.

${\displaystyle f_{L}}$ deve ser uma aplicação linear, que definimos como a diferencial de f em a.

A equação anterior é a fórmula de Taylor de primeira ordem para ${\displaystyle f{\big (}\mathbf {a} +\mathbf {v} {\big )}}$.

${\displaystyle f}$ é diferenciável em ${\displaystyle \mathbf {x} }$ com diferencial ${\displaystyle f_{L}{\big (}\mathbf {y} {\big )}\Rightarrow }$

a) ${\displaystyle \exists f'{\big (}\mathbf {x}$ ;\mathbf {y} {\big )}\quad \forall \mathbf {y} \in \mathbb {R} ^{n}}

b) ${\displaystyle f'{\big (}\mathbf {x}$ ;\mathbf {y} {\big )}=\sum _{k=1}^{n}y_{k}{\cfrac {\partial f}{\partial x_{k}}}}

${\displaystyle {\begin{array}{rl}a)&\mathbf {v} =h\mathbf {y} ,\quad h\in \mathbb {R} ,\\&\lim _{{\big \|}\mathbf {v} {\big \|}\to \mathbf {0} }f{\big (}\mathbf {x} +\mathbf {v} {\big )}=\lim _{{\big \|}\mathbf {v} {\big \|}\to \mathbf {0} }f{\big (}\mathbf {x} +h\mathbf {y} {\big )}=f{\big (}\mathbf {x} {\big )}+f_{L}{\big (}h\mathbf {y} {\big )}=\\&f{\big (}\mathbf {x} {\big )}+hf_{L}{\big (}\mathbf {y} {\big )}\Rightarrow \\&\lim _{h\to 0}{\cfrac {f{\big (}\mathbf {x} +h\mathbf {y} {\big )}-f{\big (}\mathbf {x} {\big )}}{h}}=f'{\big (}\mathbf {x}$ ;\mathbf {y} {\big )}=f_{L}{\big (}\mathbf {y} {\big )}\end{array}}}

como queríamos demonstrar.

${\displaystyle b)}$  Expressando ${\displaystyle y}$ em função de seus componentes na base

${\displaystyle {\begin{array}{l}{\big \{}\mathbf {e} _{1},\ldots ,\mathbf {e} _{n}{\big \}},f_{L}{\big (}\mathbf {y} {\big )}=f_{L}{\big (}\sum _{k=1}^{n}y_{k}\mathbf {e} _{k}{\big )}=\sum _{k=1}^{n}y_{k}f_{L}{\big (}\mathbf {e} _{k}{\big )}=\sum _{k=1}^{n}y_{k}f'{\big (}\mathbf {x}$ ;\mathbf {e} _{k}{\big )}=\\\sum _{k=1}^{n}y_{k}{\cfrac {\partial f}{\partial x_{k}}}\end{array}}}

como queríamos demonstrar.

Seja ${\displaystyle f:S\subset \mathbb {R} ^{n}\longrightarrow \mathbb {R} }$ um campo escalar e ${\displaystyle \mathbf {x} :J\in \mathbb {R} \longrightarrow S}$. Definimos a função composta ${\displaystyle g=f\circ \mathbf {x} }$ como ${\displaystyle g(t)=f{\Big [}\mathbf {x} {\big (}t{\big )}{\Big ]}}$, então ${\displaystyle \quad g'{\big (}t{\big )}=\sum _{k=1}^{n}{\cfrac {\partial f}{\partial x_{k}}}\cdot {\cfrac {dx_{k}}{dt}}}$

Seja ${\displaystyle \mathbf {f} :S\subseteq \mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{m}}$ um campo vetorial. Seja ${\displaystyle \mathbf {x} \in S}$ e ${\displaystyle \mathbf {y} }$ um vetor qualquer. Definimos a derivada

${\displaystyle \mathbf {f'} {\big (}\mathbf {x}$ ;\mathbf {y} {\big )}=\lim _{h\to 0}{\cfrac {\mathbf {f} {\big (}\mathbf {x} +h\mathbf {y} {\big )}-\mathbf {f} {\big (}\mathbf {x} {\big )}}{h}}}

Expressando ${\displaystyle \mathbf {f'} {\big (}\mathbf {x}$ ;\mathbf {y} {\big )}} em função de seus componentes, temos ${\displaystyle \mathbf {f'} {\big (}\mathbf {x}$ ;\mathbf {y} {\big )}={\Big [}f'_{1}{\big (}\mathbf {x} ;\mathbf {y} {\big )},\ldots ,f'_{m}{\big (}\mathbf {x} ;\mathbf {y} {\big )}{\Big ]}}

Dizemos que ${\displaystyle \mathbf {f} }$ é diferenciável ${\displaystyle \Leftrightarrow \exists \mathbf {f} _{L}:\mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{m}}$, aplicação linear que verifica:

${\displaystyle \lim _{{\big \|}\mathbf {v} {\big \|}\to 0}\mathbf {f} {\big (}\mathbf {x} +\mathbf {v} {\big )}=\mathbf {f} {\big (}\mathbf {x} {\big )}+\mathbf {f} _{L}{\big (}\mathbf {v} {\big )}}$.

Esta é a fórmula de Taylor de primeira ordem para ${\displaystyle \mathbf {f} .\quad \mathbf {f} _{L}{\big (}\mathbf {v} {\big )}=\mathbf {f} '{\big (}\mathbf {x}$ ;\mathbf {v} {\big )}} .

A matriz de ${\displaystyle \mathbf {f} '}$ é sua matriz jacobiana.

Se um campo vetorial ${\displaystyle \mathbf {f} }$ é diferenciável em ${\displaystyle \mathbf {x} \Rightarrow }$ é contínuo em ${\displaystyle \mathbf {x} }$.

Se deduze facilmente da fórmula de Taylor de primeira ordem já vista.

Seja ${\displaystyle \mathbf {h} {\big (}\mathbf {x} {\big )}={\big (}\mathbf {f} \circ \mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}}$ um campo vetorial definido e diferenciável em ${\displaystyle \mathbf {x} }$. Sua diferencial ${\displaystyle \mathbf {h} '{\big (}\mathbf {x} {\big )}}$ resulta ser

${\displaystyle \mathbf {h} '{\big (}\mathbf {x} {\big )}=\mathbf {f} '{\Big [}\mathbf {g} {\big (}\mathbf {x} {\big )}{\Big ]}\circ \mathbf {g} '{\big (}\mathbf {x} {\big )}}$

${\displaystyle {\cfrac {\partial ^{2}f}{\partial x_{i}\partial x_{j}}}={\cfrac {\partial ^{2}f}{\partial x_{j}\partial x_{i}}}\quad \forall i\neq j\Leftrightarrow }$ ambas derivadas parciais existem e são contínuas em ${\displaystyle \mathbf {x} }$.

Um campo escalar tem um máximo em ${\displaystyle \mathbf {x} =\mathbf {a} \Leftrightarrow }$ existe uma n-esfera ${\displaystyle B{\big (}\mathbf {a} {\big )}{\Big |}\forall \mathbf {x} \in B{\big (}\mathbf {a} {\big )}\quad f{\big (}\mathbf {x} {\big )}\leqslant f{\big (}\mathbf {a} {\big )}}$

Um campo escalar tem um mínimo em ${\displaystyle \mathbf {x} =\mathbf {a} \Leftrightarrow }$ existe uma n-esfera ${\displaystyle B{\big (}\mathbf {a} {\big )}{\Big |}\forall \mathbf {x} \in B{\big (}\mathbf {a} {\big )}\quad f{\big (}\mathbf {x} {\big )}\geqslant f{\big (}\mathbf {a} {\big )}}$

Um campo escalar tem um ponto de sela ${\displaystyle \Leftrightarrow }$

${\displaystyle \forall B{\big (}\mathbf {a} {\big )}\quad \exists \mathbf {x} {\big |}f{\big (}\mathbf {x} {\big )}\leqslant f{\big (}\mathbf {a} {\big )}\land \exists \mathbf {x} {\big |}f{\big (}\mathbf {x} {\big )}\geqslant f{\big (}\mathbf {a} {\big )}}$.

Função com um ponto de sela.

Para saber se é um dos casos anteriores:

1. Obtemos ${\displaystyle \mathbf {x} {\Big |}{\cfrac {\partial f}{\partial x_{k}}}=0\qquad \forall k{\Big |}1\leqslant k\leqslant n}$
2. Obtemos a matriz hessiana de f. Seja esta ${\displaystyle \mathbf {F} {\big (}\mathbf {x} {\big )}}$.
   1. ${\displaystyle \mathbf {F} {\big (}\mathbf {x} {\big )}}$ é definida positiva ${\displaystyle \Rightarrow f}$ tem um mínimo local (mínimo relativo) em ${\displaystyle \mathbf {x} }$.
   2. ${\displaystyle \mathbf {F} {\big (}\mathbf {x} {\big )}}$ é definida negativa ${\displaystyle \Rightarrow f}$ tem um máximo local (máximo relativo) em ${\displaystyle \mathbf {x} }$.
   3. ${\displaystyle \mathbf {F} {\big (}\mathbf {x} {\big )}}$ é indefinida ${\displaystyle \Rightarrow f}$ tem um ponto de sela em ${\displaystyle \mathbf {x} }$.

No exposto anteriormente, supomos que ${\displaystyle {\cfrac {\partial ^{2}f}{\partial x_{i}\partial x_{j}}}}$ é contínua ${\displaystyle \forall i,j{\big |}1\leqslant i\leqslant n,1\leqslant j\leqslant n}$