Espaço conexo

Em topologia, conexidade ^{(português brasileiro)} ou conectividade ^{(português europeu)} é a propriedade de um espaço conexo, isto é, um espaço topológico que não pode ser representado como a união de dois ou mais conjuntos abertos disjuntos e não-vazios.[1]

De cima para baixo: os espaços vermelho A, magenta B, amarelo C e laranja D são todos conexos, enquanto o espaço verde E (composto pelos subconjuntos E1, E2, E3 e E4) é desconexo. Para além disso, A e B são também simplesmente conexos (género 0), enquanto C e D não o são: C tem género 1 e D tem género 4.

Definição

Uma cisão de um conjunto é a decomposição $X=A\cup B$ em dois abertos disjuntos. Todo conjunto admite a cisão trivial em que $A=X$ e $B=\emptyset$ . Um conjunto chama-se conexo quando admite apenas a cisão trivial.[1]

Equivalências

Os subconjuntos $\emptyset$ e $X$ são, ao mesmo tempo, abertos e fechados em qualquer topologia de $X$ . Assim, equivalentemente, se eles são os únicos conjuntos abertos e fechados, então $X$ é conexo. Por outro lado, se existe $A$ não-vazio aberto e fechado em $X$ , então $X$ é desconexo.[2]

Exemplos

$\mathbb {R}$ e $\mathbb {C}$ são conexos, enquanto $\mathbb {N} ,$ $\mathbb {Z}$ e $\mathbb {Q}$ são desconexos.
Em $\mathbb {R}$ , os únicos subconjuntos conexos são os intervalos.[3]
$\mathbb {R} -\{0\}$ é desconexo pois possui a cisão não-trivial $(-\infty ,0)\cup (0,+\infty )$ .[1]

Propriedades

A imagem de um conexo por uma aplicação contínua é um conexo.[4]
Todo conjunto homeomorfo a um conexo é conexo.[4]
A união de uma família de conjuntos conexos que possuam um ponto em comum é conexa.[5]
O produto cartesiano de dois conjuntos é conexo se, e somente se, ambos são conexos.[5]
O fecho de um conjunto conexo é conexo.[6]

Componentes conexas

Mesmo que um conjunto $X$ não seja conexo, ele sempre poderá ser representado pela união disjunta de suas componentes conexas.[7]

A componente conexa $C_{x}$ é o maior subconjunto conexo que contém $x\in X$ .[7] Para quaisquer dois pontos de $X$ , suas componentes conexas ou coincidem ou são disjuntas. Se possuem um ponto em comum, são a mesma componente conexa, pois a componente conexa é o maior subconjunto conexo contendo um dado ponto; se não possuem, são disjuntas.[7]

Por exemplo, para $\mathbb {R} -\{0\}$ , a componente conexa de $-1$ é $(-\infty ,0)$ e a componente conexa de $1$ é $(0,+\infty )$ . No caso, essas são as duas componentes conexas do conjunto.[7]

Propriedades

Toda componente conexa de $X$ é um conjunto fechado em $X$ .[7]

Homeomorfismos estabelecem, entre os dois espaços, uma bijeção entre as componentes conexas de um com as componentes conexas do outro.[7] Sendo assim, dois conjuntos homeomorfos possuem a mesma quantidade de componentes conexas.[7]

Conexo por caminhos

Um espaço conexo por caminhos

Um espaço conexo que não é conexo por caminhos.

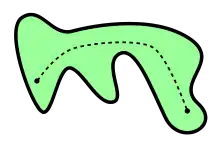
Um tipo de conexidade mais estrita é a conexidade por caminhos.[8]

Um caminho num conjunto $X\subset \mathbb {R} ^{n}$ é uma função contínua definida num intervalo real que passa por pontos de $X$ . Dois pontos podem ser ligados por um caminho quando existe um caminho $f$ tal que esses pontos estejam na imagem de $f$ .[9] Um conjunto se diz conexo por caminhos quando quaisquer dois pontos podem ser ligados por um caminho.[9]

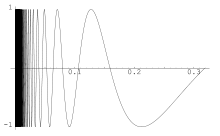
Todo conjunto conexo por caminhos é conexo, mas a recíproca é falsa.[10] Por exemplo, no $\mathbb {R} ^{2},$ o gráfico da função $f(x)={\mbox{sen}}{\frac {1}{x}}$ para $0<x\leq 1$ com a origem $(0,0)$ é conexo mas não é conexo por caminhos.[10]

Propriedades

A união de dois conjuntos conexos por caminhos, de interseção não-vazia, é conexa por caminhos.[carece de fontes]
A topologia produto de dois conjuntos conexos por caminhos é conexa por caminhos.[carece de fontes]
Todo conjunto convexo é conexo por caminhos.[11]
No $\mathbb {R} ^{n}$ , um conjunto aberto é conexo se, e somente se, é conexo por caminhos.[12]

Ver também

Conexidade simples

Referências

Lima 1981, p. 54.
Lima 1981, p. 55.
Lima 1981, p. 55, Teorema 31.
Lima 1981, p. 55, Teorema 30.
Lima 1981, p. 57, Teorema 33.
Lima 1981, p. 59, Teorema 35.
Lima 1981, p. 63.
Lima 1981, p. 59.
Lima 1981, pp. 59-60.
Lima 1981, p. 61.
Lima 1981, p. 60.
Lima 1981, p. 61, Teorema 36.

Bibliografia

Lima, Elon Lages (1981). Curso de análise, Volume 2. Instituto de Matemática Pura e Aplicada. Rio de Janeiro: Instituto de Matemática Pura e Aplicada
Munkres, James R. (2000), Topology, ISBN 9780131816299, Prentice Hall, Incorporated.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[FOOTNOTELima198154-1] Lima 1981, p. 54.

[FOOTNOTELima198155-2] Lima 1981, p. 55.

[FOOTNOTELima198155Teorema_31-3] Lima 1981, p. 55, Teorema 31.

[FOOTNOTELima198155Teorema_30-4] Lima 1981, p. 55, Teorema 30.

[FOOTNOTELima198157Teorema_33-5] Lima 1981, p. 57, Teorema 33.

[FOOTNOTELima198159Teorema_35-6] Lima 1981, p. 59, Teorema 35.

[FOOTNOTELima198163-7] Lima 1981, p. 63.

[FOOTNOTELima198159-8] Lima 1981, p. 59.

[FOOTNOTELima198159-60-9] Lima 1981, pp. 59-60.

[FOOTNOTELima198161-10] Lima 1981, p. 61.

[FOOTNOTELima198160-11] Lima 1981, p. 60.

[FOOTNOTELima198161Teorema_36-12] Lima 1981, p. 61, Teorema 36.