Conjugado harmônico projetivo

Em geometria projetiva, o ponto conjugado harmônico de um trio ordenado de pontos sobre a reta projetiva real é definido pela seguinte construção:

Dados três pontos colineares A, B, C, fazendo-se L ser um ponto não repousando sobre suas junções e fazendo-se qualquer reta através C encontrar LA, LB em M, N respectivamente. Se AN e BM encontram-se em K, e LK encontra AB em D, então D é chamado o conjugado harmônico de C em relação A, B.[1]

Referências

  1. R. L. Goodstein & E. J. F. Primrose (1953) Axiomatic Projective Geometry, University College Leicester (edição).
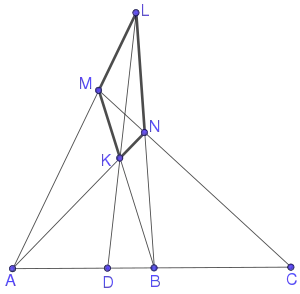
D é o conjugado harmônico de C w.r.t. A e B.
A, D, B, C formam uma série harmônica.
KLMN é um quadrângulo completo gerando-o.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.