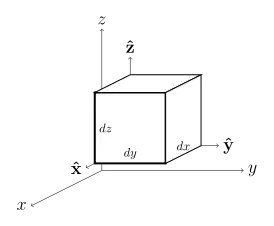
Del em coordenadas cilíndricas e esféricas
Esta é uma lista de algumas fórmulas de cálculo do vetor para trabalhar com sistemas comuns de coordenadas curvilíneas[nt 1].
Conversões de coordenadas
| De | ||||
|---|---|---|---|---|
| Cartesiano | Cilíndrico | Esférico | ||
| Para | Cartesiano | |||
| Cilíndrico | ||||
| Esférico | ||||
Conversões de vetor unitário
| Cartesiano | Cilíndrico | Esférico | |
|---|---|---|---|
| Cartesiano | não aplicável | ||
| Cilíndrico | não aplicável | ||
| Esférico | não aplicável |
| Cartesiano | Cilíndrico | Esférico | |
|---|---|---|---|
| Cartesiano | não aplicável | ||
| Cilíndrico | não aplicável | ||
| Esférico | não aplicável |
Fórmula Del
| Operação | Coordenadas cartesianas (x, y, z) | Coordenadas cilíndricas (ρ, φ, z) | Coordenadas esféricas (r, θ, φ), onde é o polar e θ é o ângulo azimutal α |
|---|---|---|---|
| campo vetorial A | |||
| Gradiente ∇f | |||
| Divergência ∇ ⋅ A | |||
| Rotacional ∇ × A | |||
| Operador de Laplace ∇2f ≡ ∆f | |||
| Vetor de Laplace ∇2A ≡ ∆A |
|
}} | |
| Derivada materialα[1] (A ⋅ ∇)B |
}} | ||
| tensor divergente ∇ ⋅ T |
|
|
|
| Deslocamento diferencial dℓ | |||
| Área normal diferencial dS | |||
| Volume diferencialdV |
- ↑α Esta página usa para o ângulo polar e para o ângulo azimutal, que é uma notação comum na física. A fonte que é usada para essas fórmulas usa para o ângulo azimutal e para o ângulo polar, que é uma notação matemática comum. Para obter as fórmulas de matemática, altere e nas fórmulas mostradas na tabela acima.
Regras de cálculo não triviais
- (Fórmula de Lagrange para del)
Derivação cilíndrica

Derivação esférica
Notas
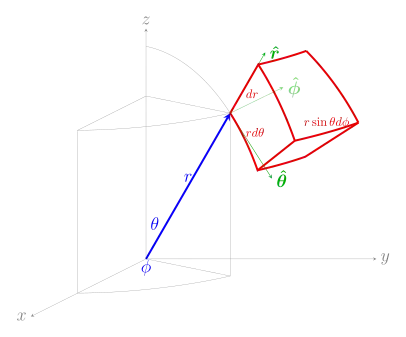
- Este artigo usa a notação padrão ISO 80000-2, que substitui a ISO 31-11, para coordenadas esféricas (outras fontes podem reverter as definições de θ e φ):
- O ângulo polar é denotado por θ: é o ângulo entre o eixo z e o vetor radial que liga a origem ao ponto em questão.
- O ângulo azimutal é denotado por φ: é o ângulo entre o eixo x e a projeção do vetor radial no plano xy.
- "curl" querer dizer "Rotacional"
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.