Divisão da circunferência em partes iguais (processo geral)

São processos do desenho geométrico que dividem a circunferência em um número "n" de partes iguais, com a utilização da régua e do compasso. Os processos dividem-se em exatos, aproximativos e gerais. O problema da divisão da circunferência se confunde com o da construção de polígonos regulares.[1] Sempre que possível é preferível que se use os processos exatos.[2]

Divisão da circunferência em 11 partes aproximadamente iguais pelo Processo Geral de Rinaldini. A ilustração mostra o hendecágono inscrito.

Processos exatos

Só são conhecidos os processos exatos para a divisão da circunferência em 2, 3, 5, 15 e 17[nota 1] lados. Obviamente os dobros também são possíveis (4, 6, 10, 30 e 34), bem como os dobros dos dobros (8, 12, 20, 60 e 68) e assim sucessivamente.[1]

Processos aproximativos

Os processos aproximativos referem-se à divisão em 7, 9, 11 e 13 partes iguais. Os dobros também funcionam para esses processos.[1]

Processos gerais

Os mais conhecidos processos gerais[1], que dividem a circunferência em número qualquer de partes iguais, são: o processo de Bion, o processo de Tempier e o processo de Rinaldini.

Processo de Rinaldini

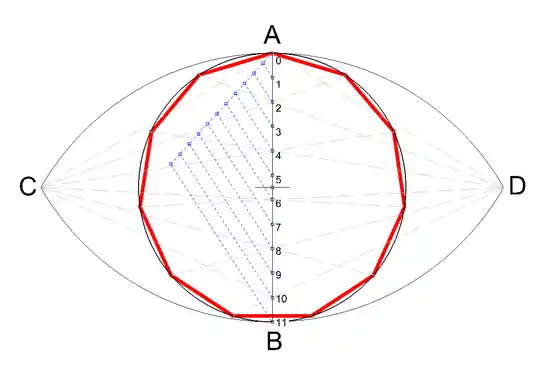
Nesta construção, a circunferência será divida em 11 partes iguais.[2]

  • Trace o diâmetro AB da circunferência a ser dividida;
  • Com a ponta seca do compasso em A e abertura AB trace um arco de circunferência;
  • Com a ponta seca do compasso em B e abertura AB trace outro arco de circunferência;
  • A interseção dos arcos determinará os pontos C e D;
  • Divida o diâmetro em 11 partes iguais;
  • Escolha os números pares ou os ímpares (na ilustração foram escolhidos os números pares);
  • Trace semirretas que partam de C e D e que passem pelos pontos 0, 2, 4, 6, 8 e 10;
  • As interseções, entre as semirretas e o lado oposto da circunferência, determinam a divisão em 11 partes aproximadamente iguais;

Processo auxiliado por computador

Os programas CAD têm comandos, como o divide, que fazem a divisão exata de quaisquer curvas, sendo elas abertas ou fechadas.[3]

Notas
[nota 1] ^ O processo de divisão em 17 partes iguais foi elaborado por Gauss. Em Disquisitiones Arithmeticae, Gauss demonstrou que os polígonos regulares de p lados, em que p é um primo de Fermat, da forma:
são construtíveis com régua e compasso. Em 1837, Pierre Wantzel mostrou que esta condição também é necessária para que o polígono regular de p lados, com p primo, seja construtível.[4]

    Referências
    1. Putnoki, José Carlos (1989). Elementos de Geometria e desenho geométrico. [S.l.]: Scipione. pp. 55–64. Vol. 2
    2. Mandarino, Denis (2007). Desenho geométrico, construções com régua e compasso. [S.l.]: Plêiade. pp. 57–65
    3. andrew.cmu.edu. «AutoCAD 2D Tutorial» (PDF). Consultado em 25 de Maio de 2012
    4. Tom Rike, Oakland High School, Gauss and the Heptadecagon Arquivado em 20 de julho de 2010, no Wayback Machine. [em linha]

    Bibliografia
    • Theodoro, Braga (1997). Desenho linear geométrico. São Paulo: Cone
    • Carvalho, Benjamim (1982). Desenho Geométrico. São Paulo: Ao Livro Técnico
    • Giongo, Affonso Rocha (1954). Curso de Desenho Geométrico. São Paulo: Nobel
    • Marmo, Carlos (1995). Desenho Geométrico. São Paulo: Scipione

    Ver também

    Ligações externas
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.