Equação de Antoine

A equação de Antoine é um tipo de semicorrelação empírica que descreve a relação entre pressão de vapor e temperatura de substâncias puras. A equação de Antoine é derivada da relação de Clausius–Clapeyron. A equação foi apresentada em 1888 pelo engenheiro francês Louis Charles Antoine.[1]

A equação

\log _{10}p=A-{\frac {B}{C+T}}

onde $p$ é a pressão de vapor, $T$ é a temperatura e $A$ , $B$ e $C$ são parâmetros constantes específicos para uma determinada substância.

A forma simplificada com C igual a zero é chamada de equação de August, em referência ao físico alemão Ernst Ferdinand August:

\ln p=A-{\frac {B}{T}}

A equação de August descreve uma relação linear entre o logaritmo da pressão e a recíproca da temperatura. Isso pressupõe uma entalpia de vaporização independente da temperatura. A equação de Antoine permite uma descrição melhorada, porém ainda inexata, da alteração da entalpia de vaporização com a temperatura.

A equação de Antoine também pode ser expressa com a temperatura explícita a partir de simples manipulações algébricas:

T={\frac {B}{A-\ln p}}-C

Intervalo de validade

Por não ser suficientemente flexível, a equação de Antoine não pode ser usada para descrever toda a curva de pressão de vapor saturado, do ponto triplo até o ponto crítico. Por conta disso, vários conjuntos de parâmetros para uma única substância são comumente usados. Um conjunto de parâmetros para pressão baixa é usado para descrever a curva de pressão de vapor até o ponto de ebulição normal, enquanto um segundo conjunto de parâmetros é usado para o intervalo do ponto de ebulição normal até o ponto crítico.

Desvios típicos de um ajuste de parâmetros em função da temperatura (dados experimentais para o benzeno). Quanto mais parâmetros, menor o desvio
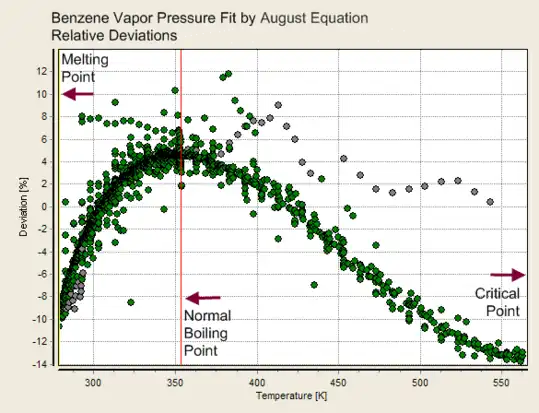Desvios de um ajuste da equação de Antoine (dois parâmetros)
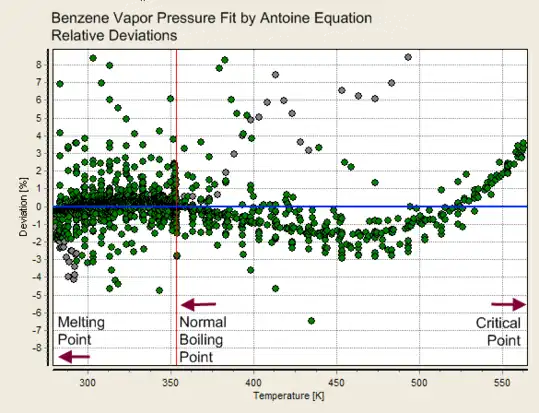Desvios de um ajuste da equação de Antoine (três parâmetros)
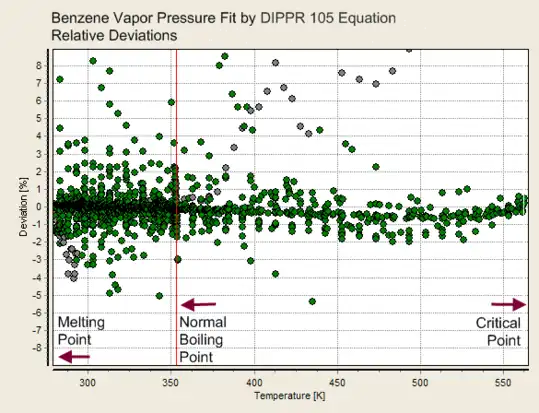Desvios de um ajuste da equação DIPPR 101 (quatro parâmetros)

Exemplos de parâmetros

Substância	A	B	C	T min. °C	T máx. °C
Água	8,07131	1730,63	233,426	1	100
Água	8,14019	1810,94	244,485	99	374
Etanol	8,20417	1642,89	230,300	-57	80
Etanol	7,68117	1332,04	199,200	77	243

Os parâmetros são dadas em °C e mmHg.

Exemplo de cálculo

O ponto de ebulição normal do etanol é $T B$ = 78,32 °C. Usando o primeiro e o segundo conjunto de parâmetros para o etanol, respectivamente, tem-se que:

P=10^{(8{,}20417-{\frac {1642{,}89}{78{,}32+230{,}300}})}=760{,}0\ \mathrm {mmHg}

P=10^{(7{,}68117-{\frac {1332{,}04}{78{,}32+199{,}200}})}=761{,}0\ \mathrm {mmHg}

(760 mmHg = 101,325 kPa = 1,000 atm = pressão normal)

Esse exemplo mostra um grave problema causado pelo uso de dois diferentes conjuntos de parâmetros. A pressão de vapor descrita não é contínua no ponto de ebulição normal, forencendo dois valores diferentes para a dita pressão. Isso gera grandes problemas para técnicas computacionais que dependem de uma curva de pressão de vapor contínua.

Existem duas soluções possíveis: a primeira abordagem utiliza apenas um conjunto de parâmetros para um grande intervalo de temperatura, aceitando o desvio característico entre os valores de pressão de vapor real e o valor calculado. Uma variante dessa abordagem é pela utilização de um conjunto especial de parâmetros ajustado para a faixa de temperatura examinada. A segunda solução é utilizar uma equação de pressão de vapor com mais de três parâmetros. As equações comumente utilizadas para isso são extensões simples da equação de Antoine, como a equação de DIPPR ou de Wagner.[2][3]

Unidades

Os coeficientes da equação de Antoine são normalmente dados em mmHg, ainda que atualmente o Sistema Internacional de Unidades (SI) recomende o uso de pascal. O uso de unidades anteriores ao SI tem razões históricas, devido ao uso original por Antoine.

No entanto, é fácil converter os parâmetros de pressão e temperatura para diferentes unidades. Para mudar de graus Celsius para kelvin, basta subtrair 273,15 do parâmetro $C$ . Para mudar de milímetros de mercúrio para pascal, é necessário adicionar o logaritmo comum do fator de conversão entre as duas unidades ao parâmetro $A$ :

$A_{\mathrm {Pa} }=A_{\mathrm {mmHg} }+\log _{10}{\frac {101325}{760}}=A_{\mathrm {mmHg} }+2.124903.$

Os parâmetros em °C e mmHg para o etanol no intervalo de -57 a 80°C:

A	B	C
8,20417	1642,89	230,300

quando convertidos para K e Pa resultam em:

A	B	C
10,32907	1642,89	-42,85

\log _{10}(P)=10{,}3291-{\frac {1642{,}89}{351{,}47-42{,}85}}=5{,}005727378=\log _{10}(101328\ \mathrm {Pa} ).

Uma transformação igualmente simples pode ser feita ao trocar o logaritmo comum pelo logaritmo natural, ou seja, multiplicando os parâmetros $A$ e $B$ pelo ln(10) = 2.302585.

Convertendo os parâmetros do etanol originais para K e Pa utilizando o método acima:

A	B	C
23,7836	3782,89	-42,85

\ln P=23{,}7836-{\frac {3782{,}89}{351{,}47-42{,}85}}=11{,}52616367=\ln(101332\,\mathrm {Pa} ).

Extensão da equação de Antoine

Para superar os limites da equação de Antoine, ela pode ser estendida pelo uso de termos adicionais:

P=\exp {\left(A+{\frac {B}{C+T}}+D\cdot T+E\cdot T^{2}+F\cdot \ln \left(T\right)\right)}

P=\exp \left(A+{\frac {B}{C+T}}+D\cdot \ln \left(T\right)+E\cdot T^{F}\right)

Os parâmetros adicionais aumentam a flexibilidade da equação e permitem a descrição de toda a curva de pressão de vapor. As formas estendidas da equação podem ser reduzidas para a forma original igualando-se os parâmetros adicionais $D$ , $E$ e $F$ a 0.

Uma outra diferença é que as equações estendidas usam o número de Euler (e) como base para a função exponencial e o logaritmo natural. Isso não afeta a forma da equação.

Ver também

Correlação de Lee–Kesler

Referências

Antoine, C. (1888), «Tensions des vapeurs; nouvelle relation entre les tensions et les températures» [Vapor Pressure: a new relationship between pressure and temperature], Comptes Rendus des Séances de l'Académie des Sciences (em francês), 107: 681–684, 778–780, 836–837
Wagner, W. (1973), «New vapour pressure measurements for argon and nitrogen and an new method for establishing rational vapour pressure equations», Cryogenics, 13 (8): 470–482, Bibcode:1973Cryo...13..470W, doi:10.1016/0011-2275(73)90003-9
Reid, Robert C.; Prausnitz, J. M.; Sherwood, Thomas K. (1977), Properties of Gases and Liquids, ISBN 978-007051790-5 3rd ed. , New York: McGraw-Hill

Bibliografia

NIST Chemistry WebBook
Dortmund Data Bank
Diretório de livros de referência e bancos de dados contendo parâmetros de Antoine
Vários livros de referência e publicações:
- Lange's Handbook of Chemistry, McGraw-Hill Professional
- Wichterle I., Linek J., "Antoine Vapor Pressure Constants of Pure Compounds"
- Yaws C. L., Yang H.-C., "To Estimate Vapor Pressure Easily. Antoine Coefficients Relate Vapor Pressure to Temperature for Almost 700 Major Organic Compounds", Hydrocarbon Processing, 68(10), Pages 65–68, 1989

Ligações externas

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Antoine, C. (1888), «Tensions des vapeurs; nouvelle relation entre les tensions et les températures» [Vapor Pressure: a new relationship between pressure and temperature], Comptes Rendus des Séances de l'Académie des Sciences (em francês), 107: 681–684, 778–780, 836–837

[2] Wagner, W. (1973), «New vapour pressure measurements for argon and nitrogen and an new method for establishing rational vapour pressure equations», Cryogenics, 13 (8): 470–482, Bibcode:1973Cryo...13..470W, doi:10.1016/0011-2275(73)90003-9

[3] Reid, Robert C.; Prausnitz, J. M.; Sherwood, Thomas K. (1977), Properties of Gases and Liquids, ISBN 978-007051790-5 3rd ed. , New York: McGraw-Hill