Função hiperbólica inversa

Na matemática, a função hiperbólica inversa fornece um ângulo hiperbólico correspondente a um determinado valor da função hiperbólica. A magnitude do ângulo hiperbólico é equivalente à área do setor hiperbólico da hipérbole unitária xy = 1, ou o dobro da área correspondente ao setor da unidade x² − y² = 1, assim como um ângulo circular é o dobro da área do setor circular de um círculo unitário.[1]

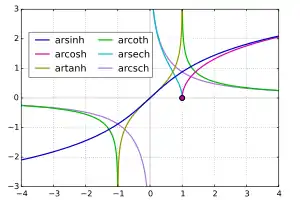
Gráficos da função hiperbólica inversa quanto às funções trigonométricas inversas.

Quanto à nomenclatura, as abreviaturas preferenciais são arsinh, arcosh e assim por diante, sendo estas representantes das funções trigonométricas inversas. Em outros campos, tal como a ciência da computação, a abreviação é feita pelo prefixo asinh e ainda pode ser válido as notações sinh⁻¹(x), cosh⁻¹(x), entre outras.[2]

Representação logarítmica

Arco seno hiperbólico

\operatorname {arsinh} x=\ln(x+{\sqrt {x^{2}+1}})

O domínio é o conjunto de números reais.

Demonstração:

$x={\frac {e^{y}-e^{-y}}{2}}\Longleftrightarrow 2xe^{y}=(e^{y})^{2}-1$

Se $z=e^{y}\ ,\ y=\ln(z)$ então $2xz=z^{2}-1\Longleftrightarrow z^{2}-2xz-1=0$

$z_{1,2}={\frac {2x\pm {\sqrt {4x^{2}+4}}}{2}}\ =x\pm {\sqrt {x^{2}+1}}\Longleftrightarrow y_{1,2}=\ln(x\pm {\sqrt {x^{2}+1}})$

Como $x-{\sqrt {x^{2}+1}}<0$ , a única solução será $\ln(x+{\sqrt {x^{2}+1}})$ .

Arco cosseno hiperbólico

\operatorname {arcosh} x=\ln(x+{\sqrt {x^{2}-1}})

O domínio é o intervalo fechado $[1, +\infty )$ .

Demonstração:

$x={\frac {e^{y}+e^{-y}}{2}}\ <==>\ 2xe^{y}=(e^{y})^{2}+1$

Se $z=e^{y}\ ,\ y=\ln(z)$ então $2xz=z^{2}+1\ <==>\ z^{2}-2xz+1=0\ <==>\$

$z_{1,2}={\frac {2x\pm {\sqrt {4x^{2}-4}}}{2}}\ =x\pm {\sqrt {x^{2}-1}}\ <==>\ y_{1,2}=\ln(x\pm {\sqrt {x^{2}-1}})$

Como $x-{\sqrt {x^{2}-1}}={\frac {1}{x+{\sqrt {x^{2}-1}}}}$ a solução será $\pm \ln(x+{\sqrt {x^{2}-1}})$ . Após uniformização, temos $\ln(x+{\sqrt {x^{2}-1}})$

Arco tangente hiperbólica

\operatorname {artanh} x={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)

O domínio é o intervalo aberto $(-1, 1)$ .

Arco cotangente hiperbólica

\operatorname {arcoth} x={\frac {1}{2}}\ln \left({\frac {x+1}{x-1}}\right)

O domínio é a união dos intervalos $(-\infty, -1)$ e $(1, +\infty)$ .

Arco cossecante hiperbólica

\operatorname {arcsch} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right)=\ln \left({\frac {1+{\sqrt {1+x^{2}}}}{x}}\right)

O domínio é o conjunto dos números reais excluindo o 0.

Arco secante hiperbólica

\operatorname {arsech} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\right)

O domínio é o intervalo semiaberto $(0, 1]$ .

Note que devemos considerar o valor principal das raízes quadradas e da função logarítmica citadas acima. No caso de argumentos reais (z = x, onde x é real), algumas simplificações podem ser feitas, como por exemplo, ${\sqrt {x+1}}{\sqrt {x-1}}={\sqrt {x^{2}-1}}$ e $\ln \left({1+x}\right)-\ln \left({1-x}\right)=\ln \left({\tfrac {1+x}{1-x}}\right)$ .

Fórmulas aditivas

$\operatorname {arsinh} \;u\pm \operatorname {arsinh} \;v=\operatorname {arsinh} \left(u{\sqrt {1+v^{2}}}\pm v{\sqrt {1+u^{2}}}\right)$

$\operatorname {arcosh} \;u\pm \operatorname {arcosh} \;v=\operatorname {arcosh} \left(uv\pm {\sqrt {(u^{2}-1)(v^{2}-1)}}\right)$

$\operatorname {artanh} \;u\pm \operatorname {artanh} \;v=\operatorname {artanh} \left({\frac {u\pm v}{1\pm uv}}\right)$

${\begin{aligned}\operatorname {arsinh} \;u+\operatorname {arcosh} \;v&=\operatorname {arsinh} \left(uv+{\sqrt {(1+u^{2})(v^{2}-1)}}\right)\\&=\operatorname {arcosh} \left(v{\sqrt {1+u^{2}}}+u{\sqrt {v^{2}-1}}\right)\end{aligned}}$

Outras identidades

${\begin{aligned}2\operatorname {arcosh} x&=\operatorname {arcosh} (2x^{2}-1)&\quad {\hbox{ para }}x\geq 1\\4\operatorname {arcosh} x&=\operatorname {arcosh} (8x^{4}-8x^{2}+1)&\quad {\hbox{ para }}x\geq 1\\2\operatorname {arsinh} x&=\operatorname {arcosh} (2x^{2}+1)&\quad {\hbox{ para }}x\geq 0\\4\operatorname {arsinh} x&=\operatorname {arcosh} (8x^{4}+8x^{2}+1)&\quad {\hbox{ para }}x\geq 0\end{aligned}}$

$\ln(x)=\operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)$

Derivadas das funções hiperbólicas inversas

Derivada de arco seno hiperbólico

${\frac {d}{dx}}\,\operatorname {arsinh} \,x={\frac {1}{\sqrt {x^{2}+1}}}$

Derivada de arco cosseno hiperbólico

${\frac {d}{dx}}\,\operatorname {arcosh} \,x={\frac {1}{\sqrt {x^{2}-1}}}$ , se $1<x$

Derivada de arco tangente hiperbólico

${\frac {d}{dx}}\,\operatorname {artanh} \,x={\frac {1}{1-x^{2}}}$ , se $-1<x<1$

Derivada de arco cotangente hiperbólico

${\frac {d}{dx}}\,\operatorname {arcoth} \,x={\frac {1}{1-x^{2}}}$ , se $\left\vert x\right\vert >1$

Derivada de arco secante hiperbólico

${\frac {d}{dx}}\,\operatorname {arsech} \,x=-{\frac {1}{x{\sqrt {1-x^{2}}}}}$ , se $0<x<1$

Derivada de arco cossecante hiperbólico

${\frac {d}{dx}}\,\operatorname {arcsch} \,x=-{\frac {1}{|x|{\sqrt {1+x^{2}}}}}$ , se $x\not =0$

Expansões em série

Expansão em série de arco seno hiperbólico:

${\begin{aligned}\operatorname {arsinh} \,x&=x-\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}$

Expansão em série de arco cosseno hiperbólico:

${\begin{aligned}\operatorname {arcosh} \,x&=\ln(2x)-\left(\left({\frac {1}{2}}\right){\frac {x^{-2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-6}}{6}}+\cdots \right)\\&=\ln(2x)-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-2n}}{2n}},\qquad x>1\end{aligned}}$

Expansão em série de arco tangente hiperbólico:

${\begin{aligned}\operatorname {artanh} \,x&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}$

Expansão em série de arco cossecante hiperbólico:

${\begin{aligned}\operatorname {arcsch} \,x=\operatorname {arsinh} {\frac {1}{x}}&=x^{-1}-\left({\frac {1}{2}}\right){\frac {x^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}$

Expansão em série de arco secante hiperbólico:

${\begin{aligned}\operatorname {arsech} \,x=\operatorname {arcosh} {\frac {1}{x}}&=\ln {\frac {2}{x}}-\left(\left({\frac {1}{2}}\right){\frac {x^{2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{6}}{6}}+\cdots \right)\\&=\ln {\frac {2}{x}}-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n}}{2n}},\qquad 0<x\leq 1\end{aligned}}$

Expansão em série de arco cotangente hiperbólico:

${\begin{aligned}\operatorname {arcoth} \,x=\operatorname {artanh} {\frac {1}{x}}&=x^{-1}+{\frac {x^{-3}}{3}}+{\frac {x^{-5}}{5}}+{\frac {x^{-7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}$

Representação gráfica

Square representing central portion of the complex z-plane painted in psychedelic colours

\operatorname {arsinh} (z)

\operatorname {arcosh} (z)

\operatorname {artanh} (z)

\operatorname {arcoth} (z)

\operatorname {arsech} (z)

\operatorname {arcsch} (z)

Funções hiperbólicas inversas no plano-z complexo: a cor em cada ponto do plano representa o valor complexo da respectiva função que condiciona tal ponto.

Referências

«Cap. XXV. Funções hiperbólicas e funções hiperbólicas inversas». Universidade Federal Fluminense. Consultado em 28 de novembro de 2014
Amália, Luiza. «Definição: Funções Hiperbólicas» (PDF). Campus Experimental de Sorocaba. Universidade Estadual Paulista. Consultado em 28 de novembro de 2014

Ligações externas

Hazewinkel, Michiel, ed. (2001), «Inverse hyperbolic functions», Enciclopédia de Matemática, ISBN 978-1-55608-010-4 (em inglês), Springer

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] «Cap. XXV. Funções hiperbólicas e funções hiperbólicas inversas». Universidade Federal Fluminense. Consultado em 28 de novembro de 2014

[2] Amália, Luiza. «Definição: Funções Hiperbólicas» (PDF). Campus Experimental de Sorocaba. Universidade Estadual Paulista. Consultado em 28 de novembro de 2014