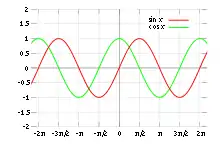
Função periódica

Um função ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$ é dita periódica de período T (ou apenas T-periódica) se existe um número real T tal que ${\displaystyle f(x+T)=f(x)}$ para todo x real.[1]

Observe que se uma função tem período T então ${\displaystyle f(x+nT)=f(x)}$ para todo n inteiro, ou seja, é também periódica de período nT, pois:

${\displaystyle f(x)=f(t+T)=f(t+2T)=f(t+3T)=...=f(t+nT)}$

A função constante ${\displaystyle f(x)=c}$ é T-periódica para qualquer ${\displaystyle T>0}$.

O conjunto dos períodos de uma função ${\displaystyle f(x)}$, ${\displaystyle \mathbb {T}$ :=\{T\in \mathbb {R} :\forall x\in \mathbb {R} ,f(x+T)=f(x)\}} , pode ser vazio, discreto ou denso em ${\displaystyle \mathbb {R} }$. Se esse conjunto for vazio, a função é aperiódica, se for discreto então pode ser escrito na forma ${\displaystyle \{nT_{f},n\in \mathbb {Z} \}}$ onde ${\displaystyle T_{f}}$ é um real positivo, chamado de período fundamental.

Um exemplo de função periódica não constante com períodos densos em ${\displaystyle \mathbb {R} }$ é a função indicadora de ${\displaystyle \mathbb {Q} }$ em ${\displaystyle \mathbb {R} }$, definida como:

• ${\displaystyle \mathrm {X} _{\mathbb {Q} }(x)=\left\{{\begin{array}{ll}1,&x\in \mathbb {Q} \\0,&c.c.\end{array}}\right.}$

Para tanto, temos o seguinte teorema: Se ${\displaystyle f(t)}$é uma função integrável T-periódica, então o valor da integral definida dentro de um período não depende do ponto inicial, ou seja:

${\displaystyle \int _{x}^{x+T}f(t)dt}$ não depende de x.

Portanto, temos a seguinte identidade:

${\displaystyle \int _{0}^{T}f(t)dt=\int _{-T/2}^{T/2}f(t)dt}$

Demonstração[2]: Escrevemos ${\displaystyle {\tfrac {x}{T}}=n+a}$como um número inteiro ${\displaystyle n}$mais uma parte fracionária ${\displaystyle a\in [0,1)}$e concluímos que podemos escrever ${\displaystyle x=nT+y}$, onde ${\displaystyle y=aT}$, isto é, ${\displaystyle 0\leq y\leq T}$.

${\displaystyle I=\int _{x}^{x+T}f(t)dt=\int _{nT+y}^{(n+1)T+y}f(t)dt}$

${\displaystyle =\int _{nT+y}^{(n+1)T}f(t)dt+\int _{(n+1)T}^{(n+1)T+y}f(t)dt}$

Mudança de variáveis ${\displaystyle t=nT}$ e ${\displaystyle t=(n+1)T+v}$:

${\displaystyle I=\int _{y}^{T}f(u+nT)du+\int _{0}^{y}f(v+(n+1)T)dv}$

Da periodicidade, temos que ${\displaystyle f(u)=f(u+nT)}$e ${\displaystyle f(v)=f(v+(n+1)T):}$

${\displaystyle I=\int \limits _{y}^{T}f(u)du+\int _{0}^{y}f(v)dv}$

${\displaystyle =\int _{0}^{y}f(v)dv+\int _{y}^{T}f(u)du}$

Como u e v são variáveis mudas, as integrais envolvidas podem ser escritas em termos de t da seguinte forma:

${\displaystyle I=\int _{0}^{y}f(t)dt+\int _{y}^{T}f(t)dt}$

${\displaystyle =\int _{0}^{T}f(t)dt}$

O conjunto das funções periódicas de um certo período ${\displaystyle T}$ formam uma álgebra, ou seja, se ${\displaystyle f(x)}$ e ${\displaystyle g(x)}$ são T-periódicas, então:

I) ${\displaystyle \displaystyle f(x)+g(x)}$ é T-periódica

II) ${\displaystyle \displaystyle \alpha f(x)}$ é T-periódica para todo ${\displaystyle \alpha }$ real

III) ${\displaystyle \displaystyle f(x)*g(x)}$ é T-periódica

possui ainda a propriedade de ser fechado em relação à translação:

Iv) ${\displaystyle \displaystyle f(x+h)}$ é T-periódica

O mesmo pode não acontecer quando não tentamos realizar as mesmas operações com função periódicas de períodos diferentes. Exemplo:

${\displaystyle \displaystyle \sin(x)}$ e ${\displaystyle \displaystyle \sin(\pi x)}$ são periódicas com período ${\displaystyle \displaystyle 2\pi }$ e ${\displaystyle \displaystyle 2}$, respectivamente. No entanto ${\displaystyle \displaystyle \sin(x)+\sin(\pi x)}$ é aperiódica.

Se uma função ${\displaystyle f(x)}$ é T-periódica e integrável, podemos definir sua média como:

${\displaystyle \mu ={\frac {1}{T}}\int _{0}^{T}f(x)dx}$

Para toda função real periódica com período fundamental ${\displaystyle \displaystyle T_{f}>0}$, definimos a sua frequência ${\displaystyle f}$ e sua velocidade angular ${\displaystyle \omega }$ como:

• ${\displaystyle f={\frac {1}{T}}}$ e
• ${\displaystyle \omega ={\frac {2\pi }{T}}=2\pi f}$

Por consequência[2],

A soma de funções periódicas é uma não é uma função periódica;

Seja ${\displaystyle f(x)}$uma função real par diferenciável, então ${\displaystyle f'(x)=0.}$

A única função real par e ímpar é a função ${\displaystyle f(x)=0.}$

Toda função real pode ser escrita de forma única como a soma de uma função ímpar e outra par.

Em análise complexa, existem funções meromorfas que são duplamente periódicas, ou seja:

${\displaystyle f(x+T_{1})=f(x+T_{2})=f(x){\mbox{ sendo }}T_{1}{\mbox{ e }}T_{2}}$ números complexos cuja razão não é um número real.

As funções elípticas são exemplos de funções duplamente periódicas.

funções inteiras não constantes, no entanto, não podem ser duplo periódicas com períodos ${\displaystyle T_{1}}$e ${\displaystyle T_{2}}$ linearmente independentes nos reais. Pois tais funções seriam inevitavelmente limitadas.