Grafo de Biggs-Smith
No campo da matemática da teoria dos grafos o grafo de Biggs–Smith é um grafo não-orientado 3-regular com 102 vértices e 153 arestas.[1]
| Grafo de Biggs–Smith | |
|---|---|
 O grafo de Biggs–Smith | |
| vértices | 102 |
| arestas | 153 |
| Raio | 7 |
| Diâmetro | 7 |
| Cintura | 9 |
| Automorfismos | 2448 (PGL(2,17)) |
| Número cromático | 3 |
| Índice cromático | 3 |
| Propriedades | Cúbico Hamiltoniano simétrico distância-regular |
Ele tem número cromático 3, índice cromático 3, raio 7, diâmetro 7 e cintura 9. É tanto 3-vértice-conectado quanto 3-aresta-conectado.
Todos os grafos distância-regular cúbicos são conhecidos.[2] O grafo Biggs–Smith é um destes 13 grafos.
Propriedades algébricas
O grupo de automorfismo do grafo de Biggs–Smith é um grupo de ordem 2448[3] isomórfico ao PGL(2,17). Ele age transitivamente sobre os vértices, nas arestas e nos arcos do grafo. Portanto, o grafo de Biggs–Smith é im grafo simétrico. Ele tem automorfismos que levam qualquer vértice para qualquer outro vértice e qualquer aresta para qualquer outra aresta. De acordo com o censo de Foster, o grafo de Biggs-Smith, referenciado como F102A, é o único grafo cúbico simétrico em 102 vértices.[4]
O grafo de Biggs–Smith é também singularmente determinado por seu espectro de grafo, o conjunto de autovalores do grafo de sua matriz de adjacência.[5]
O polinômio característico do grafo de Biggs–Smith é: .
Galeria
 O número cromático do grafo de Biggs–Smith graph é 3.
O número cromático do grafo de Biggs–Smith graph é 3. O índice cromático do grafo de Biggs–Smith graph é 3.
O índice cromático do grafo de Biggs–Smith graph é 3.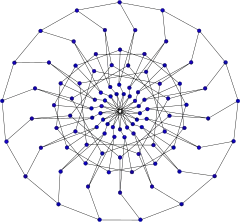 Desenho alternativo do grafo de Biggs–Smith.
Desenho alternativo do grafo de Biggs–Smith.
Referências
- Weisstein, Eric W. «Biggs–Smith Graph» (em inglês). MathWorld
- Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance-Regular Graphs. New York: Springer-Verlag, 1989.
- Royle, G. F102A data[ligação inativa]
- Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41–63, 2002
- E. R. van Dam and W. H. Haemers, Spectral Characterizations of Some Distance-Regular Graphs. J. Algebraic Combin. 15, pages 189–202, 2003