J-invariante

Em matemática, Klein j-invariante[nota 1], tida como uma função de uma variável complexa τ, é uma função modular definida sobre o semiplano superior de números complexos.[1][2]

Nós temos:

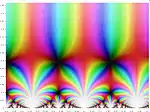
Klein j-invariante em um plano complexo.

${\displaystyle j(\tau )=1728{g_{2}^{3} \over \Delta }.}$

O discriminante modular ${\displaystyle \Delta }$ é definido como

${\displaystyle \Delta =g_{2}^{3}-27g_{3}^{2}.\,}$

O numerador e denominador acima são em termos dos invariantes modulares ${\displaystyle g_{2}}$ and ${\displaystyle g_{3}}$ das Funções elípticas de Weierstrass.

${\displaystyle g_{2}=60\sum _{(m,n)\neq (0,0)}(m+n\tau )^{-4},\qquad g_{3}=140\sum _{(m,n)\neq (0,0)}(m+n\tau )^{-6}}$

e o discriminante modular.

Estes têm as propriedades que

${\displaystyle g_{2}(\tau +1)=g_{2}(\tau ),\;g_{2}(-\tau ^{-1})=\tau ^{4}g_{2}(\tau )\,}$

${\displaystyle \Delta (\tau +1)=\Delta (\tau ),\;\Delta (-\tau ^{-1})=\tau ^{12}\Delta (\tau )\,}$

e possuem as propriedades analíticas, tornando-os formas modulares. Δ  é uma forma modular de peso 12 pelo demonstrado acima, e ${\displaystyle g_{2}}$ um de peso 4, de modo que o sua terceira potência é também de peso 12. O quociente é, portanto, uma função de modular de peso zero, o que significa j tem a propriedade absolutamente invariante que

${\displaystyle j(\tau +1)=j(\tau ),\;j(-\tau ^{-1})=j(\tau ).}$

Notas

Referências