Limites de integração
Na análise matemática e no cálculo, os limites de integração da integral de uma função integrável de Riemann definida em um intervalo fechado e limitada são os números reais e .
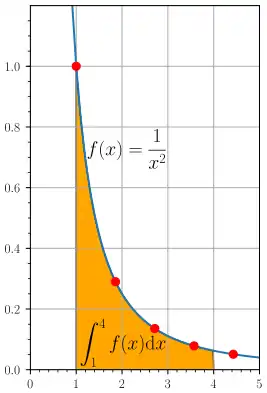
Os limites de integração são e , logo, .
Fórmula de Newton-Leibniz
Pela fórmula de Newton-Leibniz, .[1]
Em uma mudança de variável
Seja uma função contínua no intervalo e uma função contínua em , onde e e é definida e contínua no intervalo , então[3]
Exemplo
onde e . Portanto, e . Daí, os novos limites de integração são e .[4]
O mesmo se aplica a outras substituições.
Integrais impróprias
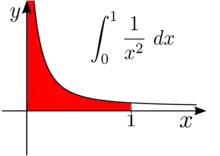
A integral é imprópria, pois e é indefinida nesse ponto.
Limites de integração também podem ser definidos para integrais impróprias, com os limites de integração de ambos[3]
- e
novamente sendo e . Para uma integral imprópria
- ou
os limites da integração são e , ou e , respectivamente.
Referências
- «Newton-Leibniz formula - Encyclopedia of Mathematics». www.encyclopediaofmath.org. Consultado em 28 de outubro de 2019
- «31.5 Setting up Correct Limits of Integration». math.mit.edu. Consultado em 30 de setembro de 2020
- Demidovǐc, Boris P.; Baranenkov, G. (1964). Problems in mathematical analysis. Moscow(IS): Moskva. ISBN 0846407612. OCLC 799468131
- «𝘶-substitution (article)». Khan Academy (em inglês). Consultado em 13 de outubro de 2020
- Weisstein, Eric W. «Definite Integral». mathworld.wolfram.com (em inglês). Consultado em 13 de outubro de 2020
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.