Par de arcos capazes

É o lugar geométrico dos pontos que enxergam um segmento AB num determinado ângulo.[1] Os pontos A e B não compartilham das propriedades do lugar geométrico.

Figura 1. Par de arcos capazes de 60º.

Por exemplo, a circunferência tem como uma de suas características ser um par de arcos capazes dos pontos que enxergam o seu diâmetro AB à 90º, excetuando-se os pontos A e B do próprio diâmetro.[2]

Processo de construção

Arcos menores do que 90º

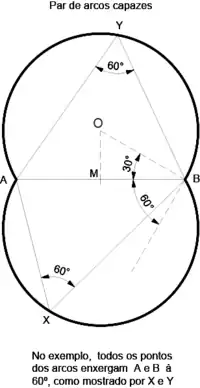
Construção do par de arcos capazes de 60º, de acordo com a figura 1:

  1. Desenhe um ângulo de 60º, tal que B seja o vértice e AB um dos segmentos que o forma.
  2. No lado oposto, trace o ângulo complementar (no caso, o de 30º)
  3. A interseção da mediatriz de AB com o lado do ângulo de 30º determina o ponto O, que é o centro do arco capaz de 60°
  4. O par de arcos capazes pode ser obtido por simetria em relação ao segmento AB.

Arcos maiores do que 90º

O arco de circunferência desprezado na construção do arco capaz de 60º, o qual completaria a circunferência, é o arco capaz do ângulo de 120º, ou seja, o que falta para 180º.

Capazoide
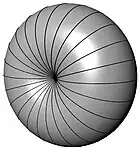
Na superfície capazoide todos os pontos da superfície enxergam o eixo de revolução num mesmo ângulo, a figura ilustra o capazoide de 30º.
Superfície capazoide de 120º.

A superfície capazoide é o lugar geométrico tridimensional dos pontos que enxergam um segmento de reta AB num mesmo ângulo. Ela é fruto da revolução (AB) do par de arcos capazes. Como na definição da Geometria plana, os pontos extremos do eixo de revolução não compartilham das propriedades do lugar geométrico.[3]

Referências
  1. Putnoki, José C. - Elementos de Geometria e desenho geométrico. Vol. 1. Ed. Scipione, São Paulo, 1989. p. 101.
  2. Putnoki, José C. - Elementos de Geometria e desenho geométrico. Vol. 1. Ed. Scipione, São Paulo, 1989. p. 103.
  3. Mandarino, Denis (12 de Julho de 2011). «Superfície capazoide». Webartigos.com. Consultado em 30 de Junho de 2012

Bibliografia

Ver também

Ligações externas
  • Alfred North Whitehead: An Introduction to Mathematics. BiblioBazaar LLC 2009 (reprint), ISBN 9781103197842, pp. 121
  • George Wentworth: Junior High School Mathematics: Book III. BiblioBazaar LLC 2009 (reprint), ISBN 9781103152360, pp. 265
  • Robert Clarke James, Glenn James: Mathematics Dictionary. Springer 1992, ISBN 9780412990410, p. 255
  • Net Saber. «Superfície capazoide». Consultado em 30 de maio de 2013
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.