Problema da ponte e da tocha

O problema da ponte e da tocha (Também conhecido como O Trem da Meia-Noite[1] e travessia perigosa[2]) é um quebra-cabeças lógico que trata de quatro pessoas, uma ponte e uma tocha. É um dos problemas da categoria dos quebra-cabeças de travessia de rio, onde um número de elementos devem mover-se através de um rio, com algumas restrições[3].

História

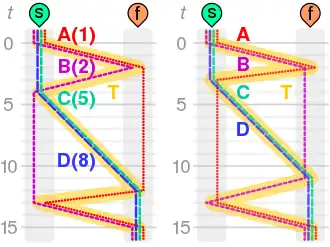
Quatro pessoas chegam a um rio no meio da noite. Há uma ponte estreita, mas ela só pode aguentar duas pessoas ao mesmo tempo. Porque é noite, a tocha deve ser usada para atravessar a ponte. A pessoa A pode atravessar a ponte em um minuto, a B em 2 minutos, a C em 5 minutos, e a D em 8 minutos. Quando duas pessoas atravessam a ponte juntos, eles devem se mover no ritmo da pessoa mais lenta. A questão é: todos eles poderão atravessar a ponte em 15 minutos ou menos?[2]

Solução

Uma idéia óbvia primeiramente é que o custo de retornar com a tocha para as demais pessoas esperando para atravessar é uma despesa inevitável que deve ser minimizada. Esta estratégia faz de A o candidato a portador da tocha, transportando cada pessoa do outro lado da ponte:

Tempo decorrido Lado inicial Ação Lado final
0 minutos A B C D
2 minutos       C D A e B cruzam o rio, levando 2 minutos A B
3 minutos A    C D A retorna, levando 1 minuto    B
8 minutos          D A e C cruzam o rio, levando 5 minutos A B C
9 minutos A       D A retorna, gastando 1 minuto    B C
17 minutos A e D cruzam o rio, levando 8 minutos A B C D

Essa estratégia não permite uma travessia em 15 minutos. Para encontrar a solução correta, é preciso perceber que forçar os dois mais lentos a atravessar o rio individualmente, desperdiça o tempo que pode ser economizado se ambos cruzarem juntos:

Tempo decorrido Lado inicial Ação Lado final
0 minutos A B C D
2 minutos       C D A e B cruzam o rio, gastando 2 minutos A B
3 minutos A    C D A retorna, gastando 1 minuto    B
11 minutos A C e D cruzam o rio, gastando 8 minutos    B C D
13 minutos A B B retorna, gastando 2 minutos       C D
15 minutos A e B cruzam o rio, gastando 2 minutos A B C D

Variações e história

Existem diversas variações, com variações estéticas, como as pessoas com nomes diferentes, ou variação nos tempos de passagem ou limite de tempo[4]. A tocha em si pode se apagar em um curto espaço de tempo e assim servir de limite de tempo. Em uma variação do chamada O Trem da Meia-Noite, por exemplo, a pessoa D precisa de 10 minutos, em vez de 8 para atravessar a ponte, e as pessoas A, B, C e D, agora chamados de quatro irmãos Gabrianni, têm 17 minutos para pegar o trem da meia-noite[1].

O quebra-cabeças é conhecido ter aparecido tão cedo quanto 1981, no livro Super Strategies For Puzzles and Games. Nesta versão do quebra-cabeça, A, B, C e D levam 5, 10, 20 e 25 minutos, respectivamente, para cruzar o rio, e o prazo é de 60 minutos[5][6]. Em todas estas variações, a estrutura e a solução do quebra-cabeças permanece a mesma.

No caso onde há um número arbitrário de pessoas com tempos arbitrários para a travessia, e a capacidade da ponte permanecendo igual a duas pessoas, o problema foi completamente analisado por métodos teoréticos de grafos[7].

Este problema tem sido usado como método para comparar a usabilidade de linguagens de programação.[8]

Ligações externas

Referências
  1. «MURDEROUS MATHS BRAINBENDERS». Consultado em 8 de fevereiro de 2008
  2. Gleb Gribakin. «Some simple and not so simple maths problems». Consultado em 8 de fevereiro de 2008
  3. PETERSON, Ivars. Science News, 164, #24 (13 de dezembro de 2003) Tricky Crossings http://www.sciencenews.org/articles/20031213/mathtrek.asp Tricky Crossings Verifique valor |url= (ajuda). Consultado em 7 de fevereiro de 2008 Em falta ou vazio |título= (ajuda)
  4. «The Bridge Crossing Puzzle». Consultado em 4 de outubro de 2010. Arquivado do original em 31 de maio de 2008
  5. SILLKE, Torsten (Setembro de 2001). «Crossing the bridge in an hour». Consultado em 9 de fevereiro de 2008
  6. LEVMORE, Saul X.; COOK, Elizabeth Early (1981). Super strategies for puzzles and games. Garden City, New York: Doubleday & Company. ISBN 0-385-17165-X
  7. ROTE, Günter (2002). «Crossing the bridge at night» (PDF). Bulletin of the European Association for Theoretical Computer Science. pp. 241–246
  8. ERWIG, Martin. «Escape from Zurg» (PDF)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.