Quarteto de Anscombe

Quarteto de Anscombe são quatro conjuntos de dados que têm estatísticas descritivas quase idênticas (como a média e a variância), mas que têm distribuições muito diferentes e aparências muito distintas quando exibidos graficamente. Cada conjunto de dados consiste de onze pontos (x,y). Eles foram construídos em 1973 pelo estatístico Francis Anscombe, com o objetivo de demonstrar tanto a importância de se visualizar os dados antes de analisá-los, quanto o efeito dos outliers e outras observações influentes nas propriedades estatísticas. Ele descreveu o artigo como tendo a finalidade de combater a impressão entre os estatísticos de que "cálculos numéricos são exatos, mas gráficos são aproximados/grosseiros."[1]

Todos os quatro conjunto de dados são idênticos quando examinado usando estatística básica, mas variam consideravelmente quando graficados.

Dados

Para os quatro conjunto de dados:

Propriedade Valor Precisão
Média de x 9 exato
Variância de x 11 exato
Média de y 7,50 até 2 casas decimais
Variância de y 4,125 ±0,003
Correlação entre x e y 0,816 até 3 casas decimais
Reta de regressão linear até 2 e 3 casas decimais, respectivamente
Coeficiente de determinação da regressão linear: 0,67 até 2 casas decimais
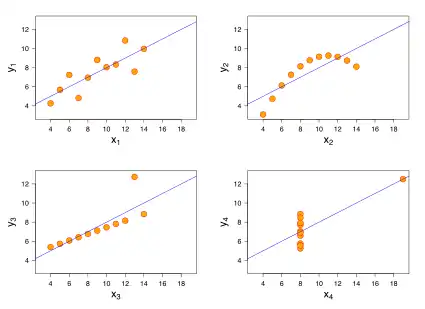
  • O primeiro gráfico de dispersão (no canto superior esquerdo) aparenta ser uma simples relação linear, correspondendo a duas variáveis correlacionadas em que y poderia ser modelado como uma gaussiana com uma média linearmente dependente de x.
  • O segundo gráfico (no canto superior direito) não mostra uma distribuição normal; enquanto a relação entre as duas variáveis é óbvia, ela não é linear, e o coeficiente de correlação de Pearson não é relevante. Uma regressão mais geral e o coeficiente de determinação correspondente seria mais apropriada.
  • No terceiro gráfico (no canto inferior esquerdo), a distribuição é linear, mas deveria ter uma reta de regressão diferente (uma regressão robusta teria sido mais apropriada). A regressão calculada está deslocada por pelo único outlier que exerce influência suficiente para reduzir o coeficiente de correlação de 1 para 0.816.
  • Finalmente, o quarto gráfico (no canto inferior direito) mostra um exemplo em que um ponto de grande alavanca é suficiente para produzir um grande coeficiente de correlação mas, embora outros pontos de dados não indiquem qualquer relação entre as variáveis.

O quarteto ainda é usado frequentemente para ilustrar a importância de visualizar um conjunto de dados graficamente antes de iniciar a análise de acordo com um tipo de relação particular, e a inadequação de propriedades estatísticas básicas para descrever conjuntos de dados realísticos.[2][3][4][5][6]

Os conjuntos de dados são os seguintes. Os valores de x são os mesmos para os três conjuntos de dados.[1]

Quarteto de Anscombe
I II III IV
x y x y x y x y
10,08,0410,09,1410,07,468,06,58
8,06,958,08,148,06,778,05,76
13,07,5813,08,7413,012,748,07,71
9,08,819,08,779,07,118,08,84
11,08,3311,09,2611,07,818,08,47
14,09,9614,08,1014,08,848,07,04
6,07,246,06,136,06,088,05,25
4,04,264,03,104,05,3919,012,50
12,010,8412,09,1312,08,158,05,56
7,04,827,07,267,06,428,07,91
5,05,685,04,745,05,738,06,89

Não se sabe como Anscombe criou seus conjuntos de dados.[7] Desde sua publicação, foram desenvolvidos vários métodos para produzir conjuntos de dados similares com estatísticas idênticas e gráficos distintos.[7][8]

Referências
  1. Anscombe, F. J. (1973). «Graphs in Statistical Analysis». American Statistician. 27 (1): 17–21. JSTOR 2682899. doi:10.1080/00031305.1973.10478966
  2. Elert, Glenn. «Linear Regression». The Physics Hypertextbook
  3. Janert, Philipp K. (2010). Data Analysis with Open Source Tools. [S.l.]: O'Reilly Media. pp. 65–66. ISBN 0-596-80235-8
  4. Chatterjee, Samprit; Hadi, Ali S. (2006). Regression Analysis by Example. [S.l.]: John Wiley and Sons. p. 91. ISBN 0-471-74696-7
  5. Saville, David J.; Wood, Graham R. (1991). Statistical Methods: The geometric approach. [S.l.]: Springer. p. 418. ISBN 0-387-97517-9
  6. Tufte, Edward R. (2001). The Visual Display of Quantitative Information 2nd ed. Cheshire, CT: Graphics Press. ISBN 0-9613921-4-2
  7. Chatterjee, Sangit; Firat, Aykut (2007). «Generating Data with Identical Statistics but Dissimilar Graphics: A follow up to the Anscombe dataset». The American Statistician. 61 (3): 248–254. JSTOR 27643902. doi:10.1198/000313007X220057
  8. Matejka, Justin; Fitzmaurice, George (2017). «Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing». Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems: 1290-1294. doi:10.1145/3025453.3025912
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.