Relação de Stifel

Não há segredos na relação de Stifel. É possível demonstrá-la recorrendo-se apenas a definição dos símbolos ${\displaystyle {\binom {n}{k}}}$, que denotam os coeficientes binomiais, e efetuando umas poucas manipulações algébricas:

${\displaystyle {\binom {n-1}{k-1}}+{\binom {n-1}{k}}={\frac {(n-1)!}{(n-k)!(k-1)!}}+{\frac {(n-1)!}{(n-k-1)!k!}}}$

${\displaystyle ={\frac {(n-1)!k}{(n-k)!(k-1)!k}}+{\frac {(n-k)(n-1)!}{(n-k)(n-k-1)!k!}}={\frac {(k+(n-k))(n-1)!}{(n-k)!k!}}}$

${\displaystyle ={\frac {n(n-1)!}{(n-k)!k!}}={\frac {n!}{(n-k)!k!}}={\binom {n}{k}}.}$

Contudo, mesmo sendo esta demonstração algébrica elementar, há uma outra demonstração que, do ponto de vista da elegância, é certamente mais atraente:

Ilustra a prova combinatória:${\displaystyle {\binom {4}{1}}+{\binom {4}{2}}={\binom {5}{2}}.}$

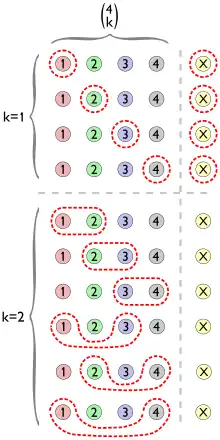
Alternativamente a demonstração algébrica oferecida, a relação de Stifel possui uma conhecida demonstração combinatória:

Seja ${\displaystyle X}$ um conjunto finito não-vazio com ${\displaystyle n}$ elementos. O número de subconjuntos de ${\displaystyle X}$ que possuem ${\displaystyle 1\leq k\leq n}$ elementos é justamente ${\displaystyle {\binom {n}{k}}}$, isto é,

${\displaystyle \#\{Y:(Y\subseteq X)\land (\#Y=k)\}={\binom {n}{k}}.}$

Por outro lado, destacando um elemento ${\displaystyle x^{\ast }\in X}$, podemos determinar o cardinal ${\displaystyle \#\{Y:(Y\subseteq X)\land (\#Y=k)\}}$ de uma maneira alternativa, procedendo como segue:

• Contamos o número de subconjuntos de ${\displaystyle X}$ com ${\displaystyle k}$ elementos que possuem ${\displaystyle x^{\ast }}$, isto é, determinamos

${\displaystyle \#\{Y\cup \{x^{\ast }\}:(Y\subseteq X\setminus \{x^{\ast }\})\land (\#Y=k-1)\}=:m_{1};}$

• Contamos o número de subconjuntos de ${\displaystyle X}$ com ${\displaystyle k}$ elementos que não possuem ${\displaystyle x^{\ast }}$, isto é, determinamos

${\displaystyle \#\{Y:(Y\subseteq X\setminus \{x^{\ast }\})\land (\#Y=k)\}=:m_{2};}$

• Somamos os dois números. Seguirá então, pelo argumento de dupla contagem, que

${\displaystyle m_{1}+m_{2}=\#\{Y:(Y\subseteq X)\land (\#Y=k)\}={\binom {n}{k}}.}$

Agora, como ${\displaystyle \#(X\setminus \{x^{\ast }\})=\#X-\#\{x^{\ast }\}=n-1}$, segue que

${\displaystyle m_{1}={\binom {n-1}{k-1}}}$

e

${\displaystyle m_{2}={\binom {n-1}{k}},}$

donde ganha-se a relação.

A relação de Stiefel, que é uma afirmação sobre coeficientes binomiais, pode ser estendida para coeficientes multinomiais:

Para quaisquer naturais ${\displaystyle n,m,k_{1},k_{2},\ldots ,k_{m}}$ tais que ${\displaystyle m\geq 2}$, ${\displaystyle 1\leq k_{i}\leq n}$ para cada ${\displaystyle i\in \{1,2,\ldots ,m\}}$ e ${\displaystyle k_{1}+k_{2}+\cdots +k_{m}=n}$

${\displaystyle {\binom {n-1}{k_{1}-1,k_{2},\ldots ,k_{m}}}+{\binom {n-1}{k_{1},k_{2}-1,\ldots ,k_{m}}}+\cdots +{\binom {n-1}{k_{1},k_{2},\ldots ,k_{m}-1}}={\binom {n}{k_{1},k_{2},\ldots ,k_{m}}}.}$

No caso em que ${\displaystyle m=2}$, fazendo a identificação ${\displaystyle k_{1}:=k}$ temos que ${\displaystyle k_{1}+k_{2}=n}$ implica ${\displaystyle k_{2}=n-k}$. Assim, usando as identificações

${\displaystyle {\binom {n-1}{k_{1}-1,k_{2}}}={\binom {n-1}{k-1,n-k}}:={\binom {n-1}{k-1}}}$

e

${\displaystyle {\binom {n-1}{k_{1},k_{2}-1}}={\binom {n-1}{k,n-k-1}}:={\binom {n-1}{k}},}$

recupera-se imediatamente a relação de Stifel para coeficientes binomiais.

Demonstração: Sejam ${\displaystyle m\geq 2}$ um natural e ${\displaystyle n,k_{1},k_{2},\ldots ,k_{m}}$ naturais tais que ${\displaystyle 1\leq k_{i}\leq n}$, para cada índice ${\displaystyle 1\leq i\leq m}$, e ${\displaystyle k_{1}+k_{2}+\cdots +k_{m}=n}$. Então

${\displaystyle {\binom {n-1}{k_{1}-1,k_{2},\ldots ,k_{m}}}+{\binom {n-1}{k_{1},k_{2}-1,\ldots ,k_{m}}}+\cdots +{\binom {n-1}{k_{1},k_{2},\ldots ,k_{m}-1}}}$

${\displaystyle ={\frac {(n-1)!}{(k_{1}-1)!k_{2}!\cdots k_{m}!}}+{\frac {(n-1)!}{k_{1}!(k_{2}-1)!\cdots k_{m}!}}+\cdots +{\frac {(n-1)!}{k_{1}!k_{2}!\cdots (k_{m}-1)!}}}$

${\displaystyle ={\frac {k_{1}(n-1)!}{k_{1}!k_{2}!\cdots k_{m}!}}+{\frac {k_{2}(n-1)!}{k_{1}!k_{2}!\cdots k_{m}!}}+\cdots +{\frac {k_{m}(n-1)!}{k_{1}!k_{2}!\cdots k_{m}!}}={\frac {(k_{1}+k_{2}+\cdots +k_{m})(n-1)!}{k_{1}!k_{2}!\cdots k_{m}!}}}$

${\displaystyle ={\frac {n(n-1)!}{k_{1}!k_{2}!\cdots k_{m}!}}={\frac {n!}{k_{1}!k_{2}!\cdots k_{m}!}}={\binom {n}{k_{1},k_{2},\ldots ,k_{m}}}.}$

• Triângulo de Pascal

• Merris, Russell (2003). Combinatorics (PDF) (em inglês). [S.l.]: John Wiley & Sons. ISBN 978-0-471-26296-1

• Pascal's rule em PlanetMath (em inglês)
• Pascal's rule proof em PlanetMath (em inglês)