Série geométrica

A série geométrica é a série que se obtém quando se tenta somar os infinitos termos de uma progressão geométrica:

\sum _{n=0}^{\infty }r^{n}=1+r+r^{2}+r^{3}+\ldots

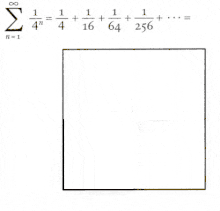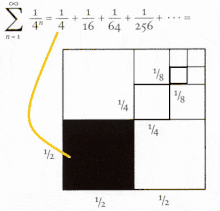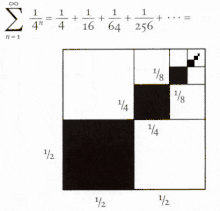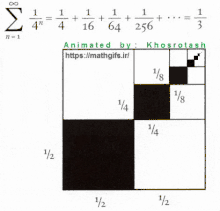
Progressão geométrica descendente com proporção de 1/4 e prova visual de que o limite da soma das frases é 1/3.

Esta série é convergente se e somente se $|r|<1$ e, neste caso, a soma vale:

\sum _{n=0}^{\infty }r^{n}={\frac {1}{1-r}}

Convergência

Da teoria das progressões geométricas, temos que:

\sum _{n=N1}^{N2}r^{n}=r^{N1}{\frac {1-r^{N2-N1+1}}{1-r}}

\sum _{n=0}^{N}r^{n}={\frac {1-r^{N+1}}{1-r}}={\frac {1}{1-r}}-{\frac {r^{N+1}}{1-r}}

É fácil ver que se $|r|<1$ então esta série é convergente e sua soma é dada por:

\sum _{n=0}^{\infty }r^{n}={\frac {1}{1-r}}

Por outro lado, se $|r|\geq 1$ , esta série não pode ser convergente pelo teste do termo geral.

De maneira geral, para qualquer série geométrica, cujo valor da Razão r seja menor que 1, sua soma é dada por:

\sum _{n=0}^{\infty }ar^{n}={\frac {a}{1-r}}

Onde "a" é o termo inicial da série.

Podemos utilizar esta série para calcular algumas séries de Taylor:

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.