Teorema de Wallace–Bolyai–Gerwien
Em geometria, o teorema de Wallace–Bolyai–Gerwien,[1] cujo nome faz referência a William Wallace, Farkas Bolyai e Paul Gerwien, afirma que quaiquer dois polígonos simples de mesma área são equidecomponíveis; isto é, pode-se cortar o primeiro em finitas peças poligonais e rearranjar as peças para obter o segundo polígono (no "rearranjo" pode-se aplicar translações e rotações).
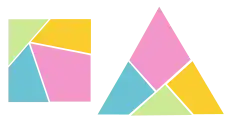
Fragmentação de um quadrado para formar um triângulo.
A generalização para poliedros foi abordada no terceiro problema de Hilbert, cuja resposta é negativa.[2]
Notas
- Este artigo foi inicialmente traduzido, total ou parcialmente, do artigo da Wikipédia em inglês cujo título é «Wallace–Bolyai–Gerwien theorem», especificamente desta versão.
Referências
Ligações externas
- Cut The Knot - Wallace–Bolyai–Gerwien Theorem
- An Example of the Bolyai–Gerwien Theorem by Sándor Kabai, Ferenc Holló Szabó, and Lajos Szilassi, the Wolfram Demonstrations Project.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.