Árvore de busca
Em ciência da computação, uma árvore de busca é uma árvore utilizada para a localização de chaves específicas dentro de um conjunto. Para que uma árvore funcione como uma árvore de busca, a chave para cada nó deve ser maior do que quaisquer chaves presentes em subárvores da esquerda e menor a quaisquer chaves em subárvores à direita.[1]
A vantagem dessas árvores está no seu eficiente tempo de busca quando a árvore está razoavelmente balanceada, o que equivale a dizer que as folhas em cada extremidade, estão em igual profundidade. Vários tipos de árvores de pesquisa existem, muitos dos quais também permitem uma eficiente inserção e exclusão de elementos.
Tipos de Árvores
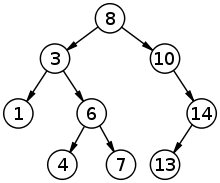
Árvore Binária De Busca
Uma Árvore binária de busca é uma estrutura de dados vinculada, baseada em nós, onde cada nó contém uma chave e duas subárvores à esquerda e a direita. Para todos nós, a chave da subárvore esquerda deve ser menor que a chave desse nó, e a chave da subárvore direita deve ser maior. Todas estas subárvores devem qualificar-se como árvores binárias de busca.
O pior caso de tempo de complexidade para a pesquisa em uma árvore binária de busca é a altura da árvore, isso pode ser tão pequeno como O(log n) para uma árvore com n elementos.
Árvore B
Árvores B são generalizações de árvores binárias de busca que podem ter um número variável de subárvores e chaves em cada nó. Mesmo que nós-filhos possuam um tamanho pré-definido, eles podem não necessariamente estar preenchidos com os dados, o que significa árvores B podem desperdiçar certo espaço. A vantagem é que as árvores B não precisam ser reequilibrados com frequência, assim como outras árvores auto-balanceadas.
Devido à faixa variável do tamanho de cada nó, árvores B são úteis para sistemas que realizam leitura de grandes blocos de dados. Elas também são muito utilizadas em bancos de dados.
O tempo de complexidade para a busca em uma árvore B é O(log n).
Árvores (a,b)
Uma árvore (a,b) é uma árvore de busca onde todas as suas folhas têm a mesma profundidade. Cada nó tem, no mínimo, a filhos e, no máximo, b filhos, enquanto que a raiz tem, no mínimo, 2 filhos e, no máximo, b filhos.
a e b podem ser decididos de acordo com a seguinte fórmula:[2]
O tempo de complexidade para o algoritimo de busca em uma árvore (a,b) é O(log n).
Árvore ternária de busca
Uma árvore ternária de busca é um tipo de trie que pode ter de 3 nós: um filho menor, um filho igual, e um filho maior. Cada nó armazena um único caractere, e a árvore em si é ordenada da mesma forma que uma árvore binária de busca é, com a exceção do possível terceiro nó.
Procurar em uma árvore ternária de busca envolve passar uma sequência de caracteres para testar se qualquer caminho a contém.
O tempo de complexidade para a busca em uma árvore ternária de busca balanceada é O(log n).