Conjuntos bem separados
Em espaços métricos, o conceito de conjuntos bem separados é mais forte que o conceito de desconexos. Dois conjuntos não vazio são ditos bem separados se a distância entre eles é positiva.
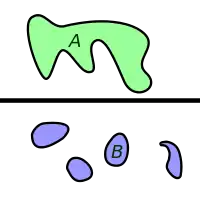
A e B são bem separados.
Definição
Seja um espaço métrico, define-se a distância entre dois subconjuntos e não-vazios de como o ínfimo das distâncias entre um ponto do conjunto e um ponto do conjunto :
Se então diz-se que e são conjuntos bem separados.
Conjuntos bem separados desconexos
Seja e conjuntos bem separados em um espaço métrico . Seja ainda:
Defina os conjuntos abertos:
onde é a bola de centro e raio definida como:
É fácil ver que e são disjuntos e ainda que e .
Propriedades
- Se e são disjuntos, e é compacto e é fechado, então e são bem separados.
- então e não são bem separados.
- Sejam e dois conjuntos bem separados em então:
- , onde é medida exterior de Lebesgue.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.