Distribuição de Gumbel

Método de Gumbel é também conhecida como método de eventos extremos ou de Ficher-Tippett. Foi desenvolvido por Emil Julius Gumbel.

Distribuição de Gumbel
Função densidade de probabilidade
Função de distribuição acumulada
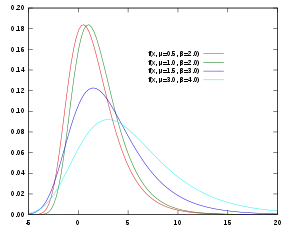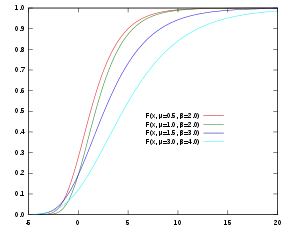Parâmetros	${\displaystyle \mu \in \mathbb {R} }$ ${\displaystyle \beta >0,}$
Suporte	${\displaystyle \mathbb {R} }$
f.d.p.	${\displaystyle {\frac {1}{\beta }}e^{-(z+e^{-z})}}$ onde ${\displaystyle z={\frac {x-\mu }{\beta }}}$
f.d.a.	${\displaystyle e^{-e^{-(x-\mu )/\beta }}}$
Média	${\displaystyle \mu +\beta \gamma }$ onde ${\displaystyle \gamma }$ é a constante de Euler-Mascheroni
Mediana	${\displaystyle \mu -\beta \ln(\ln 2)}$
Moda	${\displaystyle \mu }$
Variância	${\displaystyle {\frac {\pi ^{2}}{6}}\beta ^{2}}$
Obliquidade	${\displaystyle {\frac {12{\sqrt {6}}\,\zeta (3)}{\pi ^{3}}}\approx 1.14}$
Curtose	${\displaystyle {\frac {12}{5}}}$
Entropia	${\displaystyle \ln(\beta )+\gamma +1}$
Função Geradora de Momentos	${\displaystyle \Gamma (1-\beta t)e^{\mu t}}$
Função Característica	${\displaystyle \Gamma (1-i\beta t)e^{i\mu t}}$

É aplicada a métodos extremos, em séries anuais. Quando for de interesse estudar os valores mínimos prováveis de um fenômeno, a série deverá conter os valores mínimos de cada ano, ordenados de forma crescente; este é o caso das vazões mínimas.

Este método assume que os valores de X são limitados apenas no sentido positivo; a parte superior da distribuição X, ou seja, a parte que trata dos valores máximos mais frequentes é do tipo exponencial, a função tem a seguinte forma:

${\displaystyle P=1-e^{-e^{-y}},}$

onde Y é a variável reduzida da distribuição de Gumbel.