Estructura de Weaire-Phelan

Na geometria, a estrutura Weaire-Phelan é uma estrutura tridimensional complexa representando uma espuma idealizada de igual tamanho bolhas. Em 1993, em Trinity College, o físico Denis Weaire e seu aluno Robert Phelan constataram que, em simulações de computador de espuma, esta estrutura era uma melhor solução para o "problema de Kelvin" do que a solução mais conhecido anterior, a estrutura de Kelvin.[1]

Weaire–Phelan structure
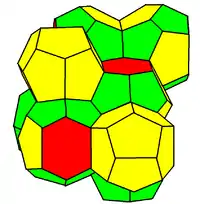Weaire–Phelan structure (polyhedral cells)
Grupo espacial
Notação de fibra dobrada
Notação de Coxeter		Pm3n (223)
2o
[[4,3,4]+]

Descrição da estrutura Weaire-Phelan

A estrutura Weaire-Phelan difere da estrutura de Kelvin na medida em que usa dois tipos de células, embora ambas têm um volume igual.

Uma delas é o pyritohedron, um dodecaedro irregular com faces pentagonais, possuindo simetria tetraédrica, (Th).[2][3][4][5] A segunda é o trapezoedro hexagonal truncado,[6][7] uma espécie de tetrakaidecaedro[8] com duas as faces hexagonais e doze pentágonos, possuindo simetria antiprismática (D2d).[9][5][10]

Referências
  1. Weaire, D.; Phelan, R. (1994), «A counter-example to Kelvin's conjecture on minimal surfaces», Phil. Mag. Lett., 69: 107–110, doi:10.1080/09500839408241577.
  2. Peter R. Cromwell, Polyhedra (1997), p. 295
  3. The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5
  4. Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
  5. N.W. Johnson: Geometries and Transformations, (2015) Chapter 11: Finite symmetry groups
  6. Wearie-Phelan Bubbles publicado pela "Steelpillow" (2006)
  7. Weaire, D., Froths, Foams and Heady Geometry, New Scientist 21 de maio de 1994.
  8. Tetrakaidecaedros (poliedros con 14 caras) por Gijs Korthals Altes (2016)
    • Coxeter, H. S. M. and Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9
  10. Conway, John Horton; Huson, Daniel H. (2002), «The Orbifold Notation for Two-Dimensional Groups», Springer Netherlands, Structural Chemistry, 13 (3): 247–257, doi:10.1023/A:1015851621002
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.