Intervalo entre primos

O primeiro, menor e único intervalo entre primos consecutivos ímpar é 1, entre o único número primo par, 2, e o primeiro número primo ímpar, 3. Todos os outros intervalos entre primos são pares, pelo fato de quaisquer dois primos consecutivos maiores que 3 terem diferença par. Existe apenas um par de intervalos entre três números naturais ímpares dos quais todos são primos. Estes intervalos são g₂ eg₃ entre os primos 3, 5 e 7 (o único par de números primos trigêmeos).

Para algum número primo P, escrevemos P# para representar P primorial, ou seja, o produto de todos os números primos menores ou iguais a P. Se Q é o número primo seguinte a P, então a sequência

${\displaystyle P\#+2,P\#+3,\ldots ,P\#+(Q-1)}$

é uma sequência Q − 2 números inteiros compostos, onde temos um intervalo entre primos de tamanho mínimo Q − 1. Portanto, existem intervalos entre primos de tamanho arbitrariamente longos, i.e., para cada número primo P, existe um inteiro n com g. Outra forma de ver que intervalos arbitrariamente grandes de primos é o fato de que a densidade de números primos se aproxima de zero, de acordo com o Teorema do Número Primo.

Na verdade, intervalos entre primos de P números podem ocorrer com números muito menores que P#. Por exemplo, a menor sequência de 71 números inteiros compostos consecutivos ocorre entre 31398 e 31468, enquanto 71# tem vinte e sete dígitos – seu valor total é 557940830126698960967415390.

Ainda que os intervalos das diferenças entre primos aumentem assintoticamente como o logaritmo neperiano, a razão dos intervalos entre primos para os inteiros decresce e assintoticamente é 0. Isso é novamente consequência do teorema do número primo.

Na direção oposta, a conjectura dos primos gêmeos afirma que g_n = 2 para infinitos valores inteiros de n.

O maior intervalo entre dois primos conhecidos até 2016 com prováveis primos identificados tem tamanho 4680156, com números primos de 99750 dígitos encontrada por Martin Raab. O maior intervalo entre dois primos com primos já provados tem tamanho 1113106, com números primos de 18662 encontrados por P. Cami, M. Jansen and J. K. Andersen.[2][3]

Dizemos que g_n é um intervalo maximal, se g_m < g_n ${\displaystyle \forall }$ m < n. O maior intervalo maximal conhecido até agosto de 2016 tem tamanho 1476, encontrado por Tomás Oliveira e Silva. É o septuagésimo-sétimo intervalo maximal, e ocorre após o número primo 1425172824437699411.[4] Outros recordes de intervalos maximais podem ser vistos em (sequência A002386 na OEIS).

Em 1931, Westzynthius provou que os intervalos entre primos cresce de forma maior do que a logarítmica. Ou seja, [5]

${\displaystyle \limsup _{n\to \infty }{\frac {g_{n}}{\log p_{n}}}=\infty .}$

Normalmente, a razão g_n / ln(p_n) é chamada de mérito de um intervalo entre primos g_n .

Maiores valores de "mérito" conhecidos (até novembro de 2016)[6][7][8]

Mérito	gn	algarismos	pn	Data	Descobridor
36,858288	10716	127	${\displaystyle {\frac {7910896513\cdot 283\#}{30}}-6480}$	2016	Dana Jacobsen
36,590183	13692	163	${\displaystyle {\frac {1037600971\cdot 383\#}{210}}-8776}$	2016	Dana Jacobsen
36,420568	26892	321	${\displaystyle {\frac {59740589\cdot 757\#}{210}}-14302}$	2016	Dana Jacobsen
35,424459	66520	816	${\displaystyle {\frac {1931\cdot 1933\#}{7230}}-30244}$	2012	Michiel Jansen
35,310308	1476	19	1425172824437699411	2009	Tomás Oliveira e Silva

Até novembro de 2016, o maior valor de "mérito" conhecido foi descoberto por Dana Jacobsen, sendo

${\displaystyle {\frac {10716}{(\ln(p_{n}))^{2}}}\approx 36,858288}$

onde 283# indica o primorial de 283.[6]

A razão de Cramér–Shanks–Granville é dada por

${\displaystyle {\frac {g_{n}}{(\ln(p_{n}))^{2}}}}$ [6]

O maior valor conhecido dessa razão é 0,9206386 para o primo 1693182318746371. Outros termos recordes estão em (sequência A111943 na OEIS).

A função de intervalo entre primos.

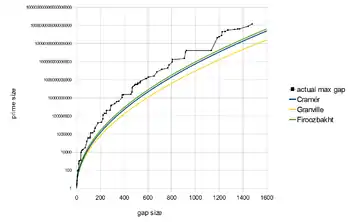
Mesmo melhores resultados estão condicionados à hipótese de Riemann. Harald Cramér demonstrou[26] que a hipótese de Riemann inplica que g_n satisfaz[27]

${\displaystyle g_{n}=O({\sqrt {p_{n}}}\log p_{n}),}$

Posteriormente, ele conjecturou que esses valores são sempre menores. Ou seja, a conjectura de Cramér utiliza a seguinte assertiva:

${\displaystyle g_{n}=O\left((\log p_{n})^{2}\right).}$

A conjectura de Firoozbakht afirma que ${\displaystyle p_{n}^{1/n}}$ (onde ${\displaystyle p_{n}}$ é o n-ésimo número primo) é uma função estritamente decrescente de n, i.e.,

${\displaystyle p_{n+1}^{1/(n+1)}<p_{n}^{1/n}\forall n\geq 1.}$

Se esta conjectura for verdadeira, então a função ${\displaystyle g_{n}=p_{n+1}-p_{n}}$ satisfaz

${\displaystyle g_{n}<(\log p_{n})^{2}-\log p_{n}{\text{ para todo }}n>4.}$[28]

Isso implica na forma forte da conjectura de Crámer, mas é inconsistente com as heurísticas de Granville e Pintz[29][30][31] que sugere que ${\displaystyle g_{n}>{\frac {2-\varepsilon }{e^{\gamma }}}(\log p_{n})^{2}}$ vale para ${\displaystyle \varepsilon >0,}$ onde ${\displaystyle \gamma }$ denota a constante de Euler-Mascheroni.

Enquanto isso, a conjectura de Oppermann é mais fraca que a conjectura de Cramér. O tamanho esperado de um intervalo entre dois primos consecutivos com a conjectura de Oppermann é da ordem de

${\displaystyle g_{n}<{\sqrt {p_{n}}}.}$

Como resultado, isso significa (assumindo a conjectura de Oppermann como verdadeira) m > 0 (provavelmente m = 30) para todo número natual n > m satisfaz ${\displaystyle g_{n}<{\sqrt {p_{n}}}.}$

A conjectura de Andrica, a qual é mais fraca que a de Oppermann, afirma que[32]

${\displaystyle g_{n}<2{\sqrt {p_{n}}}+1.}$

O tamanho do intervalo g_n entre o n-ésimo e o (n + 1)-ésimo números primos é um exemplo de função aritmética. Nesse contexto, é usualmente denotada por d_n e chamada de função diferença entre primos.[32] Esta função não aditiva nem multiplicativa. [33]

Vários tipos de programas podem ser feitos para calcular o valor de ${\displaystyle g_{n}}$, sendo um importante recurso para a matemática computacional. Abaixo, tem-se uma versão para Python, que calcula ${\displaystyle g_{n}}$ para os números primos entre 1 e 10000 (até ao número primo 9973): [33]

def prime(num):
    for divisor in range(2, num):
        if num % divisor == 0:
            return False
    return True

list_prime = []
for i in range(1,10000):
    if prime(i):
        list_prime.append(i)
        
for n in range(2, len(list_prime)):
    print(f'g({n-1}) = {list_prime[n] - list_prime[n-1]}')

• Desigualdade de Bonse
• Números primos gêmeos
• Conjectura de Goldbach

• Thomas R. Nicely, Some Results of Computational Research in Prime Numbers -- Computational Number Theory. (em inglês)
• Weisstein, Eric W. «Prime Difference Function» (em inglês). MathWorld (em inglês)
• Armin Shams, Re-extending Chebyshev's theorem about Bertrand's conjecture. (em inglês)
• www.primegaps.com Um site dedicado exclusivamente ao estudo de intervalos entre primos. (em inglês)
• Ian Stewart, Almanaque das curiosidades matemáticas. Rio de Janeiro, Zahar, 2009.
• Andrew Granville, Primes in Intervals of Bounded Length. (em inglês)