Lá menor

Em teoria musical e harmonia, Lá menor (abreviatura no sistema europeu Lá m e no sistema americano de cifras Am) é a tonalidade que consiste na escala menor baseada na nota Lá (ou nota tônica A), ou seja, é um conjunto de notas organizadas em sequencia gradual de altura,[1] e contém as notas lá, si, dó, ré, mi, fá, sol e lá, e a sua armadura não contém acidentes (sem sustenidos e sem bemóis) seguindo o padrão estrutural (ou estrutura intervalar) do modo menor (que possui cinco intervalos de tons e dois intervalos de semitons entre as notas).[2] Sua tonalidade relativa é dó maior e sua tonalidade paralela é lá maior. As alterações para as versões melódicas e harmônicas são escritas se forem necessárias.

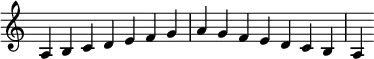
{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 7/4 a4 b c d e f g a g f e d c b a } }
Lá menor
Notação
Tonalidade
Relativa Dó maior
Homónima Lá maior
Modo Modo menor, tonalidade
Notas componentes
Lá, Si, Dó, Ré, Mi, Fá, Sol, Lá

https://upload.wikimedia.org/score/k/x/kxdqp4e8x9rtb53pex0z0rjtx37ewrj/kxdqp4e8.png

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \key c \major \time 7/4 c4 d e f g a b c b a g f e d c2 } }

No piano a escala de Lá menor não é tocado nas teclas pretas, por isso é referida como "escala das teclas brancas".

A escala relativa da escala maior, é a escala menor que inicia a partir da sexta nota (grau VI) da escala de Lá menor, neste caso é a Dó Maior; pois estas possuem a mesma armadura de clave (os mesmos acidentes sustenidos e bemóis) e as mesmas notas, são chamadas de "escalas enarmonicamente equivalentes".[3][4]

Harmonia

Graus harmônicos

Na harmonia e na teoria musical, cada grau da escala recebe um nome de acordo com a sua função exercida:[5]

Grau Nome Nota Função
I
 Tônica Lá (A) grau que determina a tonalidade da música. Tem a função de repouso natural - nota de menor tensão, geralmente apresentada no final de uma composição, passando a sensação de finalização.
II
 Supertônica Si (B) acima da tônica.[6][7] Tem duas funções resolutivas: em direção à tônica, ou em direção à mediante. Grau que substitui a subdominante.[8]
III
 Mediante Dó (C) grau intermediário formando uma terça com a tônica e a dominante. Como a subdominante, é uma nota modal, que determina se está no modo maior ou modo menor.
IV
 Subdominante Ré (D) abaixo da dominante.[9][7] Tem função de afastamento, com sentido meio-instável, uma forma intermediária sem a estabilidade da tônica e sem a angústia da dominante.
V
 Dominante Mi (E) quinto grau a partir da tônica. entre a subdominante e a superdominante.[10][11] Tem a função de tensão para a entrada da tônica, com a estabilidade.
VI
 Sobredominante Fá (F) acima da dominante.[12][7] grau intermediário (forma intervalo de terça) entre subdominante e tônica superior. Tem função fraca e, pode substituir a tônica.[8]
VII
 Sensível Sol (G) subtônica, quando o intervalo com à tônica superior é de um tom (escala menor natural); sensível quando o intervalo com à tônica superior é de um semitom (escala maior, escala menor harmônica e escala menor melódica)

Composições

Músicas eruditas em lá menor

Referências
  1. «Escala Relativa Maior E Menor». Cultura Mix. Consultado em 22 de março de 2022
  2. Lemes, Flávia (23 de agosto de 2020). «Escala maior e menor — o que são e para que servem?». Música e Vinho. Consultado em 24 de fevereiro de 2022
  3. «O que é escala relativa menor?». treinamento24.com. Consultado em 22 de março de 2022
  4. «Escalas relativas». Tecla Center. Consultado em 22 de março de 2022
  5. Santana, Beatriz Pires (2010). Os padrões que ouvimos (PDF). Universidade Federal do Paraná: Curso de Letras Português da UFPR. 24 páginas. Consultado em 10 de janeiro de 2017
  6. Santana, Beatriz Pires (2010). Os padrões que ouvimos (PDF). Universidade Federal do Paraná: Curso de Letras Português da UFPR. 24 páginas. Consultado em 10 de janeiro de 2017
  7. Silva, Ruth. «Curso de teoria musical». Academia.edu. Consultado em 10 de janeiro de 2017
  8. Rede, Itego; Governo de Goiás (2017). «Linguagem Musical III 2017» (PDF). Gabinete de Gestão de Capacitação e Formação Tecnológica. Caderno Didático. Consultado em 10 de janeiro de 2017
  9. Santana, Beatriz Pires (2010). Os padrões que ouvimos (PDF). Universidade Federal do Paraná: Curso de Letras Português da UFPR. 24 páginas. Consultado em 10 de janeiro de 2017
  10. de Oliveira, Olga Xavier. Teoria musical para crianças: Livros ou métodos infantis. Google Livros: Irmãos Vitale. 118 páginas. ISBN 9788574073767. Consultado em 10 de janeiro de 2017
  11. Adolfo, Antonio (1989). O Livro do músico. Google Livros: Irmãos Vitale. 18 páginas. ISBN 9788585426743. Consultado em 10 de janeiro de 2017
  12. Santana, Beatriz Pires (2010). Os padrões que ouvimos (PDF). Universidade Federal do Paraná: Curso de Letras Português da UFPR. 24 páginas. Consultado em 10 de janeiro de 2017
  13. Partitura da música Für Elise, de Ludwig van Beethoven - Cantorion

Ver também

Ligações externas

«Teclado musical virtual, acorde tétrade de Lá m». site Músicca

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.