Pares Ranqueados
Pares ranqueados (PR, sigla em inglês: RP) ou método de Tideman é um sistema de votação desenvolvido em 1987 por Nicolaus Tideman que seleciona um único vencedor a partir de votos que expressam preferências. PR também pode ser utilizado para gerar uma lista ordenada de vencedores.
Se há um candidato que é preferido sobre todos os outros candidatos quando comprados dois a dois, PR garante que esse candidato vencerá. Devido a essa propriedade, PR é, por definição, um método de Condorcet.
Procedimento
O procedimento para PR é o seguinte:
- Conte os votos comparando cada par de candidatos e determine o vencedor de cada par (assumindo que não há empate).
- Ordene (ranqueie) cada par por do com a maior força de vitória (mais votos ou maior diferença entre as porcentagens dos candidatos no par) para o com a menor.
- "Trave" cada par, começando por aquele que tem a maior força de vitória e continue adicionando um a um desde que eles não formem um ciclo (o que levaria a ambiguidade). O grafo completo mostra o vencedor.
Para criar uma lista ordenada de vencedores, use repetidamente o PR para selecionar um vencedor e remova esse vencedor da nova lista de candidatos e repita até a lista ficar vazia.
Contagem
Para contar os votos, consider a preferência de cada eleitor. Por exemplo, se um eleitor disser "A > B > C" (A é melhor que B, e B é melhor que C), a contagem deve adicionar um voto para A em A vs. B, um voto para A para A vs. C, e um voto em B para B vs. C. Eleitores também podem expressar indiferença (ex: A = B). Candidatos não mencionados são presumidos como sendo piores que todos os candidatos mencionados.
Com a contagem pronta, pode-se determinar as maiorias. Se "Vxy" é o número de votos em que x é preferido a y, então x vence se Vxy > Vyx, e y vence se Vyx > Vxy.
Ordenação
Os pares de vencedores, chamados de "maiorias", são então ordenados da maior para a menor. A maioria x precede a maioria y se, e somente se, uma das seguintes condições é verdadeira:
- Vxy > Vzw. Em outras palavras, a maioria que tem mais suporte para é alternativa ranqueada primeiro.
- Vxy = Vzw e Vwz > Vyx. Quando maiorias são iguais, a maioria com a menor oposição de minoria é ranqueada primeiro.[nota 1]
Travamento
A próxima etapa é examinar cada par e decidir quais devem ser "travados". Isso pode ser visualizado desenhando uma flecha do vencedor do par para o perdedor do par em um grafo orientado. Usando a lista ordenada acima, trave cada par a não ser que esse par cause uma circularidade no grafo (por exemplo, A ganha de B, B ganha de C e C ganha de A).
Vencedor
No grafo resultante, a fonte (o nó que não recebe flechas) corresponde ao vencedor. Uma fonte sempre existirá porque o grafo é, pela sua construção, um grafo acíclico orientado, e tais grafos sempre tem fontes. and such graphs always have sources. Na ausência de empates nos pares, a fonte também é única (porque sempre que dois nós parecessem ser fontes, não haveria razão válida para não conecta-los, deixando apenas um como a fonte).
Um exemplo
A situação
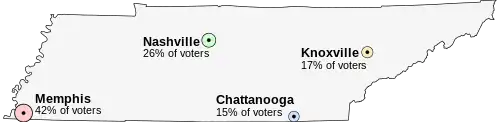
Imagine que o Tenesi, um dos estados dos Estados Unidos, está tendo uma eleição para escolher qual será a sua capital. A população do Tenesi é concentrada em torno de suas quatro maiores cidades as quais são dispersas pelo estado. Para este exemplo, suponha que o eleitorado inteiro do estado vive nessas quatro cidades e que todos querem morar tão perto da capital quanto o possível.
As quatro candidatas à capital são:
- Memphis, a maior cidade do estado, com 42% dos eleitores, mas localizada longe das demais
- Nashville, com 26% dos eleitores e no centro do estado
- Knoxville, com 17% dos eleitores
- Chattanooga, com 15% dos eleitores
As preferências dos eleitores seriam divididas assim:
| 42% dos eleitores (perto de Memphis) |
26% dos eleitores (perto de Nashville) |
15% dos eleitores (perto de Chattanooga) |
17% dos eleitores (perto de Knoxville) |
|---|---|---|---|
|
|
|
|
Os resultados seriam tabulados como abaixo:
| A | |||||
| Memphis | Nashville | Chattanooga | Knoxville | ||
| B | Memphis | [A] 58% [B] 42% |
[A] 58% [B] 42% |
[A] 58% [B] 42% | |
| Nashville | [A] 42% [B] 58% |
[A] 32% [B] 68% |
[A] 32% [B] 68% | ||
| Chattanooga | [A] 42% [B] 58% |
[A] 68% [B] 32% |
[A] 17% [B] 83% | ||
| Knoxville | [A] 42% [B] 58% |
[A] 68% [B] 32% |
[A] 83% [B] 17% |
||
| Resultado par a par (vitórias-perdas-empates): | 0-3-0 | 3-0-0 | 2-1-0 | 1-2-0 | |
| Votos contrários na pior derrota: | 58% | N/A | 68% | 83% | |
- [A] indica os eleitores que preferiram o candidato indicado na coluna em relação ao candidato indicado na linha.
- [B] indica os eleitores que preferiram o candidato indicado na linha em relação ao candidato indicado na coluna.
Contagem
Primeiramente, liste cada par e determine o vencedor:
| Par | Vencedor |
|---|---|
| Memphis (42%) vs. Nashville (58%) | Nashville 58% |
| Memphis (42%) vs. Chattanooga (58%) | Chattanooga 58% |
| Memphis (42%) vs. Knoxville (58%) | Knoxville 58% |
| Nashville (68%) vs. Chattanooga (32%) | Nashville 68% |
| Nashville (68%) vs. Knoxville (32%) | Nashville 68% |
| Chattanooga (83%) vs. Knoxville (17%) | Chattanooga: 83% |
Note que a contagem absoluta dos votos pode ser usada assim como as porcentagens. Não há diferença entre uma abordagem e outra porque o que importa é a razão dos votos entre os candidatos.
Ordenação
Os votos são então ordenados. A maior maioria é "Chattanooga melhor que Knoxville"; 83% dos eleitores preferem Chattanooga. Nashville (68%) ganha tanto de Chattanooga quanto de Knoxville com uma pontuação de 68% contra 32% (um empate, algo improvável na vida real com tantos eleitores). Como Chattanooga > Knoxville, e ambos são perdedores, Nashville vs. Knoxville será adicionado primeiro, seguido de Nashville vs. Chattanooga.
Por tanto, os pares ficam ordenados da seguinte forma:
| Par | Ganhador |
|---|---|
| Chattanooga (83%) vs. Knoxville (17%) | Chattanooga 83% |
| Nashville (68%) vs. Knoxville (32%) | Nashville 68% |
| Nashville (68%) vs. Chattanooga (32%) | Nashville 68% |
| Memphis (42%) vs. Nashville (58%) | Nashville 58% |
| Memphis (42%) vs. Chattanooga (58%) | Chattanooga 58% |
| Memphis (42%) vs. Knoxville (58%) | Knoxville 58% |
Travamento
Os pares são então travados em ordem, pulando qualquer par que geraria uma ciclo:
- Trave Chattanooga melhor que Knoxville.
- Trave Nashville melhor que Knoxville.
- Trave Nashville melhor que Chattanooga.
- Trave Nashville melhor que Memphis.
- Trave Chattanooga melhor que Memphis.
- Trave Knoxville melhor que Memphis.
Nesse caso, nenhum ciclo é criado por qualquer par, logo todos são travados.
Cada par "travado" adiciona uma flecha mostrando a relação entre os candidatos. Aqui está o grafo final: (as setas saem do ganhador e apontam para o perdedor)
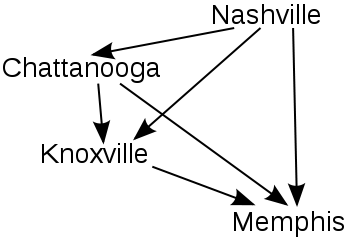
Nesse exemplo, Nashville é o ganhador usando PR, seguida por Chattanooga, Knoxville, e Memphis em segundo, terceiro, e quarto lugar respectivamente.
Exemplo de Resolução de Ambiguidade
Para uma situação simples envolvendo os candidatos A, B, e C.
- A > B: 68%
- B > C: 72%
- C > A: 52%
Nessa situação, nós "travamos" as maiorias começando com a maior primeiro.
- Trave B > C
- Trave A > B
- C > A é ignorado porque levaria a uma ambiguidade/ciclo.
Por tanto, A é o vencedor.
Resumo
Nesse exemplo de eleição, a ganhadora é Nashville. Isso seria verdade para qualquer método de Condorcet.
Usando o First-past-the-post voting e alguns outros sistemas como o de dois turnos, Memphis teria ganho a eleição por ter o maior número de votos, apesar de Nashville ter ganho cada votação simulada par a par. Usando Instant-runoff voting nesse exemplo resultaria em Knoxville ganhando apesar de mais pessoas preferirem Nashville a Knoxville.
Critérios
Dos critérios formais de votação, os método dos pares ranqueados parra o critério da maioria, o critério da monotonicidade, o critério de Smith (que implica o critério de Condorcet), o critério do perdedor de Condorcet, e o critério da independência de clones. PR falha no critério da consistência e no critério da participação. Embora PR não seja completamente independente de alternativas irrelevantes, ele satisfaz o critério da independência local de alternativas irrelevantes.
Independência de alternativas irrelevantes
PR falha no critério das alternativas irrelevantes. Entretanto, o método adere a uma propriedade menos estrita, a independência de alternativas dominadas por Smith (IADS). Ela diz que se um candidato X ganha a eleição, e uma nova alternativa Y é adicionada, X ganhará a eleição se Y não está no conjunto de Smith. IADS implica o critério de Condorcet.
Tabela de comparação
A seguinte tabela compara o método dos Pares Ranqueados com outros sistemas de votação preferencial de vencedor único:
Comparação de Sistemas de Votação Preferencial de Ganhador Único | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Monotonico | Condorcet | Maioria | Perdedor de Condorcet | Perdedor de maioria | Mutual majority | Smith | IADS | ILAI | Clone independence | Simetria reversa | Participação, Consistência | Posterior-não-atrapalha | Posterior-não-ajuda | Tempo polinomial | Resolvabilidade | |
| Schulze | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Não | Sim | Sim | Não | Não | Não | Sim | Sim |
| Pares Ranqueados | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Não | Não | Não | Sim | Sim |
| Smith alternativo | Não | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Não | Sim | Não | Não | Não | Não | Sim | Sim |
| Schwartz alternativo | Não | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Não | Sim | Não | Não | Não | Não | Sim | Sim |
| Kemeny-Young | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Não | Sim | Não | Não | Não | Não | Sim |
| Copeland | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Sim | Não | Não | Sim | Não | Não | Não | Sim | Não |
| Nanson | Não | Sim | Sim | Sim | Sim | Sim | Sim | Não | Não | Não | Sim | Não | Não | Não | Sim | Sim |
| Instant-runoff voting | Não | Não | Sim | Sim | Sim | Sim | Não | Não | Não | Sim | Não | Não | Sim | Sim | Sim | Sim |
| Borda | Sim | Não | Não | Sim | Sim | Não | Não | Não | Não | Não | Sim | Sim | Não | Sim | Sim | Sim |
| Baldwin | Não | Sim | Sim | Sim | Sim | Sim | Sim | Não | Não | Não | Não | Não | Não | Não | Sim | Sim |
| Bucklin | Sim | Não | Sim | Não | Sim | Sim | Não | Não | Não | Não | Não | Não | Não | Sim | Sim | Sim |
| Pluralidade | Sim | Não | Sim | Não | Não | Não | Não | Não | Não | Não | Não | Sim | Sim | Sim | Sim | Sim |
| Voto contingente | Não | Não | Sim | Sim | Sim | Não | Não | Não | Não | Não | Não | Não | Sim | Sim | Sim | Sim |
| Coombs[n1 1] | Não | Não | Sim | Sim | Sim | Sim | Não | Não | Não | Não | Não | Não | Não | Não | Sim | Sim |
| MiniMax | Sim | Sim | Sim | Não | Não | Não | Não | Não | Não | Não | Não | Não | Não | Não | Sim | Sim |
| Anti-pluralidade[nota 2] | Sim | Não | Não | Não | Sim | Não | Não | Não | Não | Não | Não | Sim | Não | Não | Sim | Sim |
| Sri Lankan | Não | Não | Sim | Não | Não | Não | Não | Não | Não | Não | Não | Não | Sim | Sim | Sim | Sim |
| Suplementar | Não | Não | Sim | Não | Não | Não | Não | Não | Não | Não | Não | Não | Sim | Sim | Sim | Sim |
| Dodgson[nota 2] | Não | Sim | Sim | Não | Não | Não | Não | Não | Não | Não | Não | Não | Não | Não | Não | Sim |
Notas
- De fato, existem diferentes maneiras como a "força de uma vitória" é medida.
Notas
- {{{1}}}
Bibliografia
- Tideman, T.N. (1987) Independence of clones as a criterion for voting rules. Social Choice and Welfare 4: 185-206.