Poliedros de Kepler-Poinsot
Um poliedro de Kepler-Poinsot é um poliedro regular não convexo. Todas as suas faces são polígonos regulares iguais, e em todos os vértices encontram-se o mesmo número de faces (comparar com sólidos platónicos).
.svg.png.webp)
O grande dodecaedro, um dos quatro poliedros de Kepler-Poinsot
Tabela
Existem quatro Poliedros de Kepler-Poinsot, os quais estão listados a seguir:
| Poliedro de Kepler-Poinsot | Imagem | Faces | Vértices | Arestas |
|---|---|---|---|---|
| Pequeno dodecaedro estrelado | 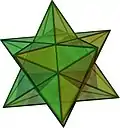 | 12 pentagramas regulares | 12 | 30 |
| Grande dodecaedro estrelado |  | 12 pentagramas regulares | 20 | 30 |
| Grande dodecaedro |  | 12 pentágonos regulares | 12 | 30 |
| Icosaedro estrelado |  | 20 triângulos equiláteros | 12 | 30 |
História
Johannes Kepler, em 1619, descobriu dois poliedros que são simultaneamente regulares e não convexos - o pequeno dodecaedro estrelado e o grande dodecaedro estrelado.
Dois séculos mais tarde provar-se-ia que existem apenas nove poliedros regulares: os cinco sólidos platónicos e quatro poliedros regulares não convexos - os poliedros de Kepler-Poinsot.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.