Raiz quadrada de um segmento

A raiz quadrada[1] de um segmento feita com régua e compasso, é construída da seguinte forma:

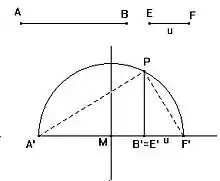
Raiz quadrada

Encontramos a soma do segmento AB com segmento unidade EF por meio de transporte de segmentos para uma reta r e marcamos como A'B' e E'F'.
Traçamos uma reta mediatriz entre os pontos A' e F' encontrando o ponto médio M.
Traçamos a semi-circunferência de centro em M e raio A'M
Traçamos uma perpendicular por B' ate encontrar a semi-circunferência marcando o ponto P.
O segmento de reta B'P' é a raiz quadrada do segmento AB.

Justificativa

O triângulo A'PF' esta inscrito em um triângulo retângulo logo B'P é uma altura relativa a hipotenusa. Assim

{\overline {B'P}}^{2}={\overline {A'B'}}.{\overline {E'F'}}\Rightarrow {\overline {B'P}}={\sqrt {{\overline {A'B'}}.{\overline {E'F'}}}}

sendo $E'F'=1$ temos que ${\overline {B'P}}={\sqrt {\overline {A'B'}}}$ logo ${\overline {B'P}}={\sqrt {\overline {AB}}}$

Ver também

Referências

Albrecht, Clarissa Ferreira. «Desenho Geométrico» (PDF). Universidade Federal de Viçosa

Bibliografia

WAGNER, Eduardo. Construções Geométricas. Rio de Janeiro: SBM, 2001.
Eduardo Wagner, Construções Geométricas, Coleção do Professor de Matemática, Sociedade Brasileira de Matemática, Rio de Janeiro, 1993.

Ligações externas

Construções Geométricas com Régua e Compasso de Alex Gomes da Silva

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.