Triângulo equilátero
Em geometria, um triângulo equilátero é todo triângulo em que os três lados são iguais, triângulos equiláteros também são equiangulares, isto é, todos os três ângulos internos são congruentes um com o outro e medem . Eles são polígonos regulares, e, portanto, podem também serem referidos como triângulos regulares.
| Triângulo equilátero | |
|---|---|
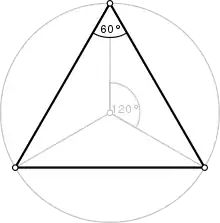 Triângulo Equilátero | |
| Tipo | Polígono regular |
| Arestas e Vértices | 3 |
| Símbolo de Schläfli | {3} |
| Diagrama de Coxeter | |
| Grupo de simetria | Diedriial (D3) |
| Área | |
| Ângulo interno (graus) | 60° |
Principais evoluções
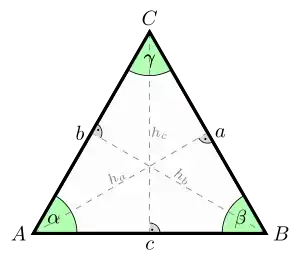
Triângulo equilátero
Assumindo que os comprimentos dos lados do triângulo são , podemos determinar através do Teorema de Pitágoras que:
- A área é
- O perímetro
- O raio do círculo circunscrito é
- O raio do círculo inscrito é
- O centro geométrico do triângulo está no centro dos círculos circunscritos e inscritos
- A altura a partir de qualquer lado é .
Muitas dessas relações podem ser escritas em função da altura (), que será comum aos três lados:
- A área é
- O lado é
- O perímetro é ou
- O raio do círculo circunscrito é
- O Apótema do círculo que circunscreve o triângulo é
- É um triângulo acutângulo.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.