Grupo diedral

• O grupo possui ${\displaystyle 2n}$ elementos: o elemento neutro, ${\displaystyle n-1}$ rotações próprias e ${\displaystyle n}$ reflexões.
• Para ${\displaystyle n>2,}$ o grupo não é abeliano.
• O subgrupo das rotações é isomorfo ao grupo cíclico ${\displaystyle \mathbb {Z} _{n},}$ e é um subgrupo normal

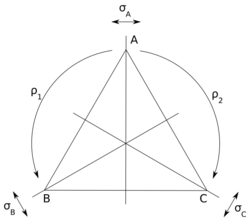
As cinco simetrias não triviais do triângulo equilátero.

Seja ABC um triângulo equilátero. Dentre as suas simetrias, temos:

• e: o elemento neutro, ou seja, a transformação identidade que leva cada ponto do triângulo nele mesmo.
• ${\displaystyle \rho _{1}}$ a rotação que leva A em B, B em C e C em A.
• ${\displaystyle \rho _{2}}$ a rotação que leva A em C, C em B e B em A.
• ${\displaystyle \sigma _{A}}$ a simetria em torno da altura que passa por A.
• ${\displaystyle \sigma _{B}}$ a simetria em torno da altura que passa por B.
• ${\displaystyle \sigma _{C}}$ a simetria em torno da altura que passa por C.

Não existem outras simetrias. Considerando * como a composição de funções, temos, por exemplo, que ${\displaystyle \sigma _{A}*\rho _{1}}$ leva A em C, B em B e C em A, ou seja, ${\displaystyle \sigma _{B}=\sigma _{A}*\rho _{1}.}$ Por outro lado, ${\displaystyle \rho _{1}*\sigma _{A}=\sigma _{C},}$ ou seja, o grupo não é abeliano. Completando as operações, chegamos à tabela:

Grupo de Simetrias do Triângulo Equilátero

${\displaystyle \star }$	e	${\displaystyle \rho _{1}}$	${\displaystyle \rho _{2}}$	${\displaystyle \sigma _{A}}$	${\displaystyle \sigma _{B}}$	${\displaystyle \sigma _{C}}$
e	e	${\displaystyle \rho _{1}}$	${\displaystyle \rho _{2}}$	${\displaystyle \sigma _{A}}$	${\displaystyle \sigma _{B}}$	${\displaystyle \sigma _{C}}$
${\displaystyle \rho _{1}}$	${\displaystyle \rho _{1}}$	${\displaystyle \rho _{2}}$	e	${\displaystyle \sigma _{C}}$	${\displaystyle \sigma _{A}}$	${\displaystyle \sigma _{B}}$
${\displaystyle \rho _{2}}$	${\displaystyle \rho _{2}}$	e	${\displaystyle \rho _{1}}$	${\displaystyle \sigma _{B}}$	${\displaystyle \sigma _{C}}$	${\displaystyle \sigma _{A}}$
${\displaystyle \sigma _{A}}$	${\displaystyle \sigma _{A}}$	${\displaystyle \sigma _{B}}$	${\displaystyle \sigma _{C}}$	e	${\displaystyle \rho _{1}}$	${\displaystyle \rho _{2}}$
${\displaystyle \sigma _{B}}$	${\displaystyle \sigma _{B}}$	${\displaystyle \sigma _{C}}$	${\displaystyle \sigma _{A}}$	${\displaystyle \rho _{2}}$	e	${\displaystyle \rho _{1}}$
${\displaystyle \sigma _{C}}$	${\displaystyle \sigma _{C}}$	${\displaystyle \sigma _{A}}$	${\displaystyle \sigma _{B}}$	${\displaystyle \rho _{1}}$	${\displaystyle \rho _{2}}$	e