Distribuição binomial negativa

A distribuição binomial negativa ou distribuição de Pascal é uma distribuição de probabilidade discreta. Esta distribuição indica o número de tentativas necessárias para obter k sucessos de igual probabilidade θ ao fim de n experimentos de Bernoulli, sendo a última tentativa um sucesso. A sua função de probabilidade é dada por:

Distribuição Binomial Negativa
Gráfico da função densidade de probabilidade para n=10 e diferentes valores de p
Gráficos da função de distribuição acumulada para n=10 e diferentes valores de p
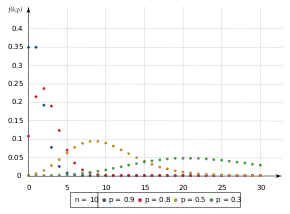
Parâmetros	${\displaystyle n\in \mathbb {N} ,n>0,}$ número de falhas até o experimento parar ${\displaystyle p\in \mathbb {R} ,0<p<1,}$ probabilidade de sucesso em cada experimento
Suporte	${\displaystyle k\in \{0,1,...\}}$ número de sucessos
f.d.p.	${\displaystyle {k+r-1 \choose k}(1-p)^{n}p^{k}}$
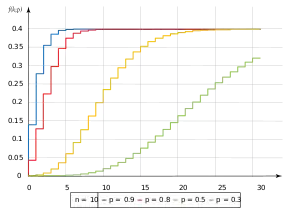
f.d.a.	${\displaystyle 1-I_{p}(k+1,n)}$, a função beta incompleta regularizada
Média	${\displaystyle {\frac {np}{1-p}}}$
Moda	${\displaystyle \lfloor {\frac {p(n-1)}{1-p}}\rfloor }$
Variância	${\displaystyle {\frac {pn}{(1-p)^{2}}}}$
Obliquidade	${\displaystyle {\frac {1+p}{\sqrt {pn}}}}$
Curtose	${\displaystyle {\frac {6}{n}}+{\frac {(1-p)^{2}}{pn}}}$
Função Geradora de Momentos	${\displaystyle \left({\frac {1-p}{1-pe^{t}}}\right)^{n}}$ para ${\displaystyle t<-log(p)}$
Função Característica	${\displaystyle \left({\frac {1-p}{1-pe^{it}}}\right)^{n}}$ para ${\displaystyle t\in \mathbb {R} }$

${\displaystyle \!\ b(n;k,\theta )={n-1 \choose k-1}\theta ^{k}(1-\theta )^{n-k},n=k,k+1,...}$

Numa linha de montagem, 10% das peças são defeituosas. A probabilidade de a quinta peça que se analisa ser a segunda defeituosa é

${\displaystyle b(5,2,0.1)={4 \choose 1}(0.1)^{2}(0.9)^{3}=0.02916}$

OBS.: A distribuição geométrica é fortemente relacionada com a distribuição binomial negativa. Naquela, queremos o número de tentativas para obter o primeiro sucesso, i.e., o tempo de espera até que se tenha o evento de importância ou sucesso.