Teorema de Bayes
Em teoria das probabilidades e estatística, o teorema de Bayes (alternativamente, a lei de Bayes ou a regra de Bayes) descreve a probabilidade de um evento, baseado em um conhecimento a priori que pode estar relacionado ao evento. O teorema mostra como alterar as probabilidades a priori tendo em vista novas evidências para obter probabilidades a posteriori.[1] Por exemplo, o teorema de Bayes pode ser aplicado ao jogo das três portas (também conhecido como problema de Monty Hall). [2]
| Teoria das probabilidades |
|---|
 |
Uma das muitas aplicações do teorema de Bayes é a inferência bayesiana, uma abordagem particular da inferência estatística. Quando aplicado, as probabilidades envolvidas no teorema de Bayes podem ter diferentes interpretações de probabilidade. Com a interpretação bayesiana de probabilidade, o teorema expressa como a probabilidade de um evento (ou o grau de crença na ocorrência de um evento) deve ser alterada após considerar evidências sobre a ocorrência deste evento. A inferência bayesiana é fundamental para a estatística bayesiana.[3]
O teorema de Bayes recebe este nome devido ao pastor e matemático inglês Thomas Bayes (1701 – 1761), que foi o primeiro a fornecer uma equação que permitiria que novas evidências atualizassem a probabilidade de um evento a partir do conhecimento a priori (ou a crença inicial na ocorrência de um evento). O teorema de Bayes foi mais tarde desenvolvido por Pierre-Simon Laplace, que foi o primeiro a publicar uma formulação moderna em 1812 em seu livro Teoria Analítica de Probabilidade, na tradução do francês. Harold Jeffreys colocou o algoritmo de Bayes e a formulação de Laplace em uma base axiomática. Jeffreys escreveu que "o teorema de Bayes é para a teoria da probabilidade o que o teorema de Pitágoras é para a geometria".[4]
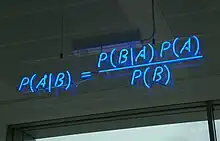
História

O teorema de Bayes recebe este nome devido ao pastor e matemático inglês Thomas Bayes (1701 – 1761), que estudou como calcular a distribuição para o parâmetro de probabilidade de uma distribuição binomial (terminologia moderna). O manuscrito não publicado de Bayes foi editado significativamente por Richard Price antes de ser lido postumamente na Royal Society. Price editou o principal trabalho de Bayes An Essay towards Solving a Problem in the Doctrine of Chances (1763),[5] que aparece em Philosophical Transactions[6] e contém o teorema de Bayes. Price escreveu uma introdução para o artigo, que fornece algumas das bases filosóficas da estatística bayesiana. Em 1765, Price foi eleito membro da Royal Society em reconhecimento ao seu trabalho sobre o legado de Bayes.[7]
O matemático francês Pierre-Simon Laplace reproduziu e estendeu os resultados de Bayes em 1774, aparentemente sem ter conhecimento do trabalho de Bayes.[8][9][10] A interpretação bayesiana da probabilidade foi desenvolvida principalmente por Laplace.[11] Stephen Stigler sugeriu em 1983 que o teorema de Bayes foi descoberto pelo matemático inglês cego Nicholas Saunderson pouco antes de Bayes.[12][13] Entretanto, esta interpretação tem sido contestada.[14] Martyn Hooper[15] e Sharon McGrayne[16] argumentaram que a contribuição de Richard Price foi substancial:
| “ | Por padrões modernos, devemos nos referir à regra Bayes–Price. Price descobriu o trabalho de Bayes, reconheceu sua importância, corrigiu–o, contribuiu para o artigo e encontrou um uso para ele. A convenção moderna de empregar apenas o nome de Bayes é injusta, mas tão arraigada que faz todo o resto não ter quase nenhum sentido.[16] | ” |
Definição formal
O teorema de Bayes é um corolário da lei da probabilidade total, expresso matematicamente na forma da seguinte equação:
,
em que e são eventos e .[17][18]
O teorema de Bayes também pode ser escrito da seguinte maneira:
- e são as probabilidades a priori de e ;
- é a probabilidade a posteriori (probabilidade condicionada) de condicional a ;
- é a probabilidade a posteriori (probabilidade condicionada) de condicional a .[17][19]
Exemplo
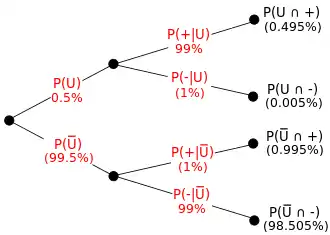
Teste de drogas
Seja um teste de drogas 99% sensível e 99% específico. Isto é, o teste produzirá 99% de resultados verdadeiros positivos para usuários de drogas e 99% de resultados verdadeiros negativos para não-usuários de drogas. Suponha que 0,5% das pessoas são usuárias de drogas. Se um indivíduo selecionado aleatoriamente testar positivo, qual a probabilidade de ele ser usuário de drogas? Isto é, qual a probabilidade de não se cometer um falso positivo?[20]
Mesmo com a aparente precisão do teste, se um indivíduo testar positivo, é mais provável que ele não seja do que ele seja usuário de drogas. Isto porque o número de não-usuários é muito maior que o número de usuários de drogas. Então, o número de falsos positivos supera o número de positivos verdadeiros. Para usar números concretos, se 1000 indivíduos forem testados, espera–se que 995 não sejam usuários e 5 sejam usuários de drogas. Para os 995 não-usuários de drogas, são esperados falsos positivos. Para os 5 usuários de drogas, são esperados positivos verdadeiros. Isto é, dos 15 resultados positivos, apenas 5 (ou 33%) são genuínos. Isto ilustra a importância da probabilidade condicional e como políticas podem ser equivocadas se as probabilidades condicionais forem negligenciadas.[21][20]
A importância da especificidade pode ser observada calculando–se que, mesmo se a sensibilidade for aumentada para 100% e a especificidade permanecer em 99%, a probabilidade do indivíduo ser um usuário de drogas subirá apenas de 33,2% para 33,4%. Entretanto, se a sensibilidade for mantida em 99% e a especificidade for aumentada para 99,5%, então a probabilidade do indivíduo ser um usuário de droga sobe para cerca de 49,9%.[20]
Interpretações
A interpretação do teorema de Bayes depende da interpretação da probabilidade atribuída aos termos. As duas interpretações principais são descritas abaixo.
Interpretação bayesiana
Na interpretação bayesiana (ou epistemológica), a probabilidade mede o grau de crença. O teorema de Bayes liga o grau de crença em uma posição antes e depois de se considerar as evidências. Por exemplo, acredita–se com 50% de certeza que uma moeda tem o dobro de probabilidade de cair cara. Se a moeda for jogada várias vezes, o grau de crença pode aumentar, diminuir ou se manter igual dependendo dos resultados observados (ver inferência bayesiana).[22]
Para proposição e evidência :
- (probabilidade a priori) é o grau de crença inicial em ;
- (probabilidade a posteriori) é o grau de crença que representa ;
- O quociente é o suporte que fornece para .[22]
Interpretação frequencista
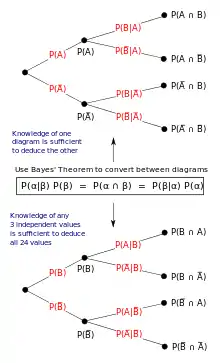
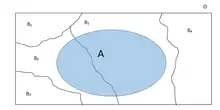
Na interpretação frequencista, a probabilidade mede uma proporção de resultados. Por exemplo, suponha-se que uma experiência seja realizada muitas vezes. é a proporção de resultados com propriedade e é a proporção de resultados com propriedade . é a proporção de resultados com propriedade , excluindo os resultados sem propriedade , e é a proporção de resultados com propriedade , excluindo os resultados sem propriedade .[23]
Probabilidades condicionais
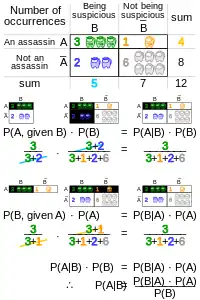
O papel do teorema de Bayes é melhor visualizado com o diagrama de árvore. Os dois diagramas dividem os mesmos resultados em e em em ordens opostas, para obter as probabilidades inversas. O teorema de Bayes serve como ligação entre estas diferentes partições.[24]
Por exemplo, um entomologista vê o que poderia ser uma rara subespécie de besouro devido a um padrão em suas costas. Nas subespécies raras, 98% dos indivíduos tem o padrão. Isto é, . Nas subespécies comuns, 5% dos indivíduos tem o padrão. Estas subespécies raras correspondem a apenas 0,1% da população. Então, qual a probabilidade do besouro com padrão ser raro? Em outras palavras, qual o valor de ?[24]
Da expressão estendida do teorema de Bayes (uma vez que qualquer besouro pode ser apenas raro ou comum), tem–se:
Isto é, o besouro com um padrão nas costas encontrado pelo entomologista tem probabilidade de 1,9% de ser raro.[24]
Formas
Forma simples
Para eventos e , dado :
.[25]
Na inferência bayesiana, deseja-se saber o grau de crença em um evento (ou conjunto de eventos) , condicionalmente à ocorrência de um evento (ou conjunto de eventos) fixado (quantidade que é conhecida como distribuição a posteriori). O teorema de Bayes mostra que a distribuição a posteriori é proporcional à probabilidade de dado (que corresponde à função de verossimilhança da amostra) vezes a probabilidade de A (chamada de probabilidade a priori ou grau de crença antes da coleta de evidências):
Forma alternativa
Outra forma do teorema de Bayes que é geralmente encontrada quando são consideradas duas afirmações ou hipóteses concorrentes é:
.[27]
Para proposição e evidência :
- (probabilidade a priori) é o grau de crença inicial em ;
- é a probabilidade correspondente do grau de crença inicial contra . ;
- (probabilidade condicional ou verossimilhança) é o grau de crença em , dado que a proposição é verdadeira;
- (probabilidade condicional ou verossimilhança) é o grau de crença em , dado que a proposição é falsa;
- (probabilidade a posteriori) é a probabilidade para , após considerar para e contra .[28]
Forma estendida
Para alguma partição do espaço amostral, muitas vezes o espaço do evento é dado em termos de e . Isto é útil para calcular , usando a lei de probabilidade total:
.[27]
Variáveis aleatórias
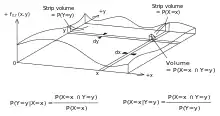
Seja o espaço amostral gerado por duas variáveis aleatórias e . Em princípio, o teorema de Bayes aplica–se aos eventos e . Entretanto, os termos se tornam 0 nos pontos em que qualquer variável tem densidade de probabilidade finita. Para continuar útil, o teorema de Bayes pode ser formulado em termos de densidades relevantes.
Forma simples
Se é contínua e é discreta,
Se é discreta e é contínua,
Se e são contínuas,
em e representam as funções de distribuição de probabilidade de e , respectivamente.[29]
Forma estendida
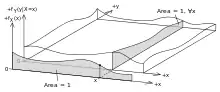
Um espaço de evento contínuo muitas vezes é dado em termos dos termos do numerador. Então, é útil eliminar o denominador usando a lei de probabilidade total. Para , isto se torna uma integral:
Regra de Bayes
A regra da Bayes é o teorema de Bayes na forma de chances:
,
em que
é chamado de fator Bayes ou razão de verossimilhança. As chances entre os dois eventos é simplesmente a razão entre as probabilidades dos dois eventos.
Então,
Portanto, a regra de Bayes afirma que as chances posteriores são as chances iniciais multiplicadas pelo fator de Bayes. Em outras palavras, as probabilidades a posteriori são proporcionais às probabilidades a priori.[30]
Derivação
Para eventos
O teorema de Bayes pode ser derivado a partir da definição de probabilidade condicional:
pois .
Então,
Logo, ajustando-se os termos, tem-se:
Para variáveis aleatórias
Para duas variáveis aleatórias contínuas e , o teorema de Bayes pode ser analogamente derivado da definição de probabilidade condicional:
Referências
- Bussab & Morettin 2010, p. 121-122.
- Neto, Joaquim (2010). «Inferência Bayesiana» (PDF). Universidade Federal de Juiz de Fora (UFJF). Consultado em 25 de maio de 2017
- Bussab & Morettin 2010, p. 317-318.
- Jeffreys, Harold (1973). Scientific Inference 3rd ed. [S.l.]: Cambridge University Press. p. 31. ISBN 978-0-521-18078-8
- Allen, Richard (1999). David Hartley on Human Nature. [S.l.]: SUNY Press. pp. 243–244. ISBN 978-0-7914-9451-6. Consultado em 16 de junho de 2013
- Bayes, Thomas; Price, Richard (1763). «An Essay towards solving a Problem in the Doctrine of Chance. By the late Rev. Mr. Bayes, communicated by Mr. Price, in a letter to John Canton, A. M. F. R. S.» (PDF). Philosophical Transactions of the Royal Society of London. 53 (0): 370–418. doi:10.1098/rstl.1763.0053. Consultado em 17 de julho de 2017. Arquivado do original (PDF) em 10 de abril de 2011
- Price, Richard (1991). Price: Political Writings. [S.l.]: Cambridge University Press. p. xxiii. ISBN 978-0-521-40969-8. Consultado em 16 de junho de 2013
- Laplace, Pierre-Simon et al. Mémoire sur la probabilité des causes par les évènements. Mémoires présentés par divers savants [à l’Académie royale des sciences], Paris, Imprimerie royale, v. 6, p. 621-656, 1774.
- Laplace, Pierre-Simon. Mémoire sur les approximations des formules qui sont fonctions de tres grands nombres. Œuvres completes X, Paris, p. 209-291, 1785.
- Daston, Lorraine (1988). Classical Probability in the Enlightenment. [S.l.]: Princeton Univ Press. p. 268. ISBN 0-691-08497-1
- Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty before 1900. Harvard University Press, Chapter 3.
- Stigler, Stephen M (1983). «Who Discovered Bayes' Theorem?». The American Statistician. 37 (4): 290–296. doi:10.1080/00031305.1983.10483122
- De Vaux, Richard; Velleman, Paul; Bock, David (2016). Stats, Data and Models 4 ed. [S.l.]: Pearson. pp. 380–381. ISBN 978-0-321-98649-8
- Edwards, A. W. F. (1986). «Is the Reference in Hartley (1749) to Bayesian Inference?». The American Statistician. 40 (2): 109–110. doi:10.1080/00031305.1986.10475370
- Hooper, Martyn (2013). «Richard Price, Bayes' theorem, and God». Significance. 10 (1): 36–39. doi:10.1111/j.1740-9713.2013.00638.x
- Mcgrayne 2011.
- Stuart, A.; Ord, K. (1994). Kendall's Advanced Theory of Statistics: Volume I—Distribution Theory. [S.l.]: Edward Arnold.
- Bussab & Morettin 2010, p. 116.
- Bussab & Morettin 2010, p. 111.
- Keedwell, Edward; Narayanan, Ajit (2005). Intelligent Bioinformatics: The Application of Artificial Intelligence Techniques to Bioinformatics Problems. [S.l.]: Joh Wiley and Sons. pp. 108 — 111. 279 páginas
- Daniel Kahneman (25 de outubro de 2011). Thinking, Fast and Slow. [S.l.]: Macmillan. ISBN 978-1-4299-6935-2. Consultado em 8 de abril de 2012
- «O Teorema de Bayes» (PDF). Universidade de São Paulo (USP). Consultado em 25 de maio de 2017
- Tripathi, Subhashini Sharma (2016). Learn Business Analytics in Six Steps Using SAS and R: A Practical, Step—by—Step to Learning Business Analytics. [S.l.]: Apress. p. 132. 218 páginas
- Farias & Laurencel 2006, p. 49-56.
- Kim, Nam-Ho; An, Dawn; Choi, Joo-Ho (2017). Prognostics and Health Management of Engineering Systems: An Introduction. [S.l.]: Springer. p. 93 — 94. 346 páginas
- Lee 2012, p. capítulo 1.
- Farias & Laurencel 2006, p. 71-72.
- Orloff, Jeremy; Bloom, Jonathan (18 de maio de 2014). «Comparison of frequentist and Bayesian inference» (PDF). MIT OCW. Consultado em 1 de junho de 2017
- Castañon, D.; Karl, W. C. (2004). SC505 Stochastic processes - Class notes. Boston: [s.n.] pp. 27–28
- Stone 2013, p. 14-15.
- Farias & Laurencel 2006, p. 41-42.
Leitura adicional
- Bruss, F. Thomas (18 de setembro de 2013). «250 years of "An essay towards solving a problem in the doctrine of chances. By the late Rev. Mr. Bayes, F.R.S. communicated by Mr. Price, in a letter to John Canton, A.M.F.R.S."». Jahresbericht der Deutschen Mathematiker-Vereinigung – Springer Journals. 115 (3-4): 129-133. doi:10.1365/s13291-013-0069-z
- Bussab, Wilton de O.; Morettin, Pedro A. (2010). Estatística Básica 6 ed. São Paulo: Saraiva. 540 páginas
- DeDeo, Simon (30 de novembro de 2016). «Bayesian Reasoning for Intelligent People» (PDF). Consultado em 8 de junho de 2016
- Farias, Ana Maria Lima de; Laurencel, Luiz da Costa (2006). «Probabilidade». Universidade Federal Fluminense (UFF)
- Gelman, Andrew; Carlin, John B.; Stern, Hal S.; Dunson, David B.; Vehtari, Aki; Rubin, Donald B. (2014). Bayesian data analysis 3 ed. Boca Raton: Chapman & Hall
- Grinstead, Charles M.; Snell, J. Laurie (2003). Introduction to Probability (PDF). [S.l.]: American Mathematical Society
- Hazewinkel, Michiel (2001). Encyclopedia of mathematics. [S.l.: s.n.]
- Laplace, Pierre-Simon (1840). Essai philosophique sur les probabilités (em francês). Paris: Bachelier
- Laplace, Pierre-Simon (1986). «Memoir on the probability of the causes of events». Statistical Science. 1 (3): 364-378. JSTOR 2245476
- Lee, Peter M (2012). Bayesian statistics: an introduction 4 ed. [S.l.]: John Wiley & Sons. 486 páginas. ISBN 978-1-118-33257-3
- Mcgrayne, Sharon B. (2011). The Theory That Would Not Die: How Bayes' Rule Cracked the Enigma Code, Hunted Down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy. London: Yale University Press. JSTOR j.ctt1np76s
- Puga, Jorge L.; Krzywinski, Martin; Altman, Naomi (2015). «Points of Significance: Bayes' theorem» (PDF). Nature Methods. 12 (4): 277-278
- Rosenthal, Jeffrey S. (2005). Struck by Lightning: The Curious World of Probabilities 1 ed. [S.l.]: HarperCollins. ISBN 978-0309097345
- Stigler, Stephen M. (1986). «Laplace's 1774 Memoir on Inverse Probability». Statistical Science. 1 (3): 359-378
- Stone, James V. (2013). Bayes' Rule: A tutorial introduction to Bayesian Analysis 1 ed. [S.l.]: Sebtel Press. ISBN 978-0-9563728-4-0
Ligações externas
- An Intuitive Explanation of Bayes' Theorem
- Bayes Theorem and the Possibility of False Claims
- Conditional Probability Explained Visually (Bayes' Theorem)
- Earliest Known Uses of Some of the Words of Mathematics (B)
- Explaining Bayesian Problems Using Visualizations
- Probability and Bayes’ Theorem
- The Mathematics of Changing Your Mind
- Weisstein, Eric W. Bayes' Theorem. From MathWorld--A Wolfram Web Resource.