Nó hiperbólico
Em matemática, um nó hiperbólico é aquele na esfera tridimensional com o complemento de um completo Riemannian metric (Variedade de Riemann) de uma curvatura constante negativa. Por exemplo, a geometria hiperbólica. Um nó hiperbólico é um nó hiperbólico com um componente.[1]
Como consequência do trabalho de William Thurston, há precisamente para cada nó os seguintes procedimentos: hiperbólico, um nó torus ou um nó satélite. Como consequência, os nós hiperbólicos podem ser considerados abundantes.[carece de fontes]
Também sobre os trabalhos de Thurston, o teorema da Cirurgia de Dehn hiperbólica que realiza as cirurgias de Dehn em um nó hiperbólica permite obter outros coletores tridimensionais hiperbólicos.[carece de fontes]
Exemplos
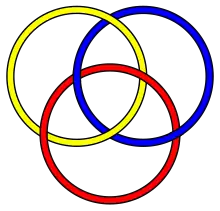
- Nó Borromeu são hiperbólicos.
- Todo non-split (não dividido), primeiro, nó alternando que não é um nó toro hiperbólico pelo resultado de William Menasco.
- 4₁ nó
- 5₂ nó
- 6₁ nó
- 6₂ nó
- 6₃ nó
- 7₄ nó
- 10 161 nó
- 12n242 nó
[carece de fontes]
Leitura complementar
- Colin Adams (1994, 2004) O Nó Livro, American Mathematical Society, ISBN 0-8050-7380-9.
- William Menasco (1984) "Fechado incompressível superfícies alternância de nó e ligação complementa", Topologia 23(1):37-44.
- William Thurston (1978-1981) , a geometria e A topologia de três variedades, Princeton anotações de aula.
Referências
- Bonnot, Sylvain (2015). «Introdução às superfícies de Riemann» (PDF). IMEUSP. Consultado em 13 de julho de 2017
Ligações externas
- Colin Adams, Hiperbólica nós (arXiv preprint)
