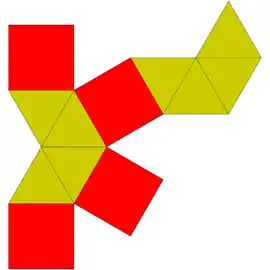
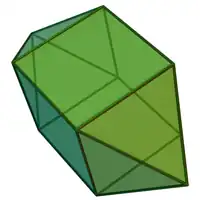
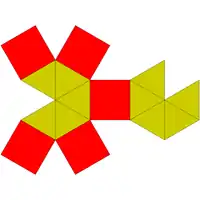
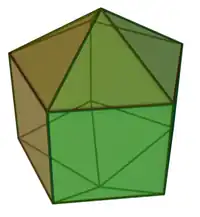
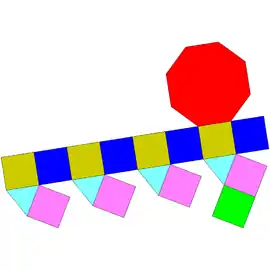
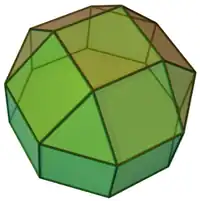
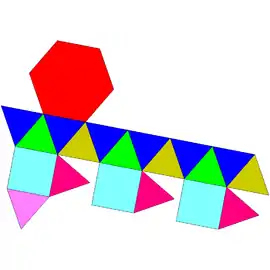
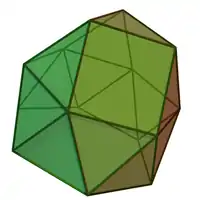
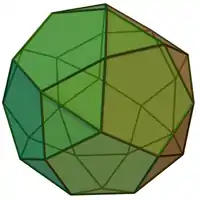
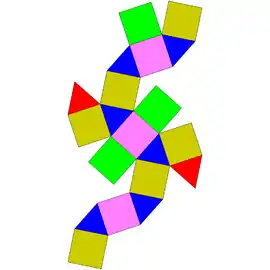
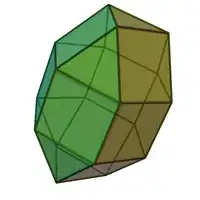
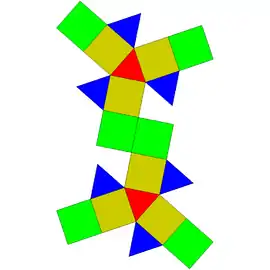
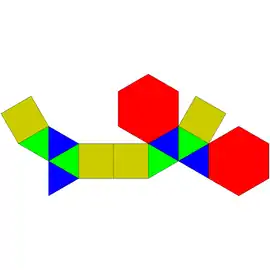
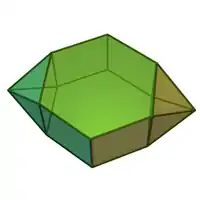
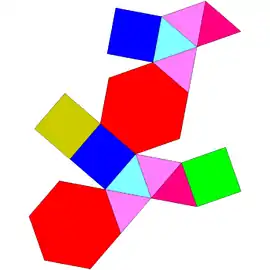
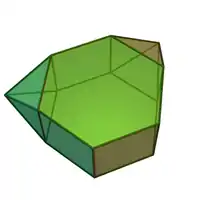
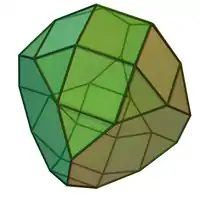
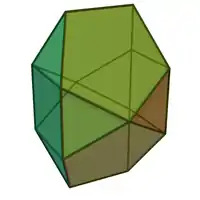
Sólidos de Johnson

Um sólido de Johnson é um Poliedro onde as faces são polígonos regulares e que não são sólidos de Platão, nem um sólido de Arquimedes, nem um prisma nem um antiprisma.

Norman Johnson elaborou uma lista de 92 sólidos em 1966, nomeou e numerou todos. Ele não provou que eram apenas 92, mas fazia ideia que eram apenas 92. Victor Zalgaller provou em 1969 que Johnson estava correto.

Lista completa

V: número de vértices,
A: número de arestas,
F: número total de faces, onde:
- F₃: número de triângulos;
- F₄: número de quadrados;
- F₅: número de pentágonos;
- F₆: número de hexágonos;
- F₈: número de octógonos;
- F₁₀: número de decágonos.

J_n	Nome	V	A	F	F₃	F₄	F₅	F₆	F₈	F₁₀	Simetría
1	pirâmide quadrada	5	8	5	4	1					C_4v
2	pirâmide pentagonal	6	10	6	5		1				C_5v
3	cúpula triangular	9	15	8	4	3		1			C_3v
4	cúpula quadrada	12	20	10	4	5			1		C_4v
5	cúpula pentagonal	15	25	12	5	5	1			1	C_5v
6	rotunda pentagonal	20	35	17	10		6			1	C_5v
7	pirâmide triangular alongada	7	12	7	4	3					C_3v
8	pirâmide quadrada alongada	9	16	9	4	5					C_4v
9	pirâmide pentagonal alongada	11	20	11	5	5	1				C_5v
10	pirâmide quadrada giralongada	9	20	13	12	1					C_4v
11	pirâmide pentagonal giralongada	11	25	16	15		1				C_5v
12	bipirâmide triangular	5	9	6	6						D_3h
13	bipirâmide pentagonal	7	15	10	10						D_5h
14	bipirâmide triangular alongada	8	15	9	6	3					D_3h
15	bipirâmide quadrada alongada	10	20	12	8	4					D_4h
16	bipirâmide pentagonal alongada	12	25	15	10	5					D_5h
17	bipirâmide quadrada giralongada	10	24	16	16						D_4d
18	cúpula triangular alongada	15	27	14	4	9		1			C_3v
19	cúpula quadrada alongada	20	36	18	4	13			1		C_4v
20	cúpula pentagonal alongada	25	45	22	5	15	1			1	C_5v
21	rotunda pentagonal alongada	30	55	27	10	10	6			1	C_5v
22	cúpula triangular giralongada	15	33	20	16	3		1			C_3v
23	cúpula quadrada giralongada	20	44	26	20	5			1		C_4v
24	cúpula pentagonal giralongada	25	55	32	25	5	1			1	C_5v
25	rotunda pentagonal giralongada	30	65	37	30		6			1	C_5v
26	girobiprisma triangular	8	14	8	4	4					D_2d
27	ortobicúpula triangular	12	24	14	8	6					D_3h
28	ortobicúpula quadrada	16	32	18	8	10					D_4h
29	girobicúpula quadrada	16	32	18	8	10					D_4d
30	ortobicúpula pentagonal	20	40	22	10	10	2				D_5h
31	girobicúpula pentagonal	20	40	22	10	10	2				D_5d
32	ortocúpula-rotonde pentagonal	25	50	27	15	5	7				C_5v
33	girocúpula-rotonde pentagonal	25	50	27	15	5	7				C_5v
34	ortobirotonde pentagonal	30	60	32	20		12				D_5h
35	ortobicúpula triangular alongada	18	36	20	8	12					D_3h
36	girobicúpula triangular alongada	18	36	20	8	12					D_3d
37	girobicúpula quadrada alongada	24	48	26	8	18					D_4d
38	ortobicúpula pentagonal alongada	30	60	32	10	20	2				D_5h
39	girobicúpula pentagonal alongada	30	60	32	10	20	2				D_5d
40	ortocúpula-rotonde pentagonal alongada	35	70	37	15	15	7				C_5v
41	girocúpula-rotonde pentagonal alongada	35	70	37	15	15	7				C_5v
42	ortobirotonde pentagonal alongada	40	80	42	20	10	12				D_5h
43	girobirotonde pentagonal alongada	40	80	42	20	10	12				D_5d
44	bicúpula triangular giralongada	18	42	26	20	6					D₃
45	bicúpula quadrada giralongada	24	56	34	24	10					D₄
46	bicúpula pentagonal giralongada	30	70	42	30	10	2				D₅
47	cúpula-rotonde pentagonal giralongada	35	80	47	35	5	7				C₅
48	birotonde pentagonal giralongada	40	90	52	40		12				D₅
49	prisma triangular aumentado	7	13	8	6	2					C_2v
50	prisma triangular biaumentado	8	17	11	10	1					C_2v
51	prisma triangular triaumentado	9	21	14	14						D_3h
52	prisma pentagonal aumentado	11	19	10	4	4	2				C_2v
53	prisma pentagonal biaumentado	12	23	13	8	3	2				C_2v
54	prisma hexagonal aumentado	13	22	11	4	5		2			C_2v
55	prisma hexagonal parabiaumentado	14	26	14	8	4		2			D_2h
56	prisma hexagonal metabiaumentado	14	26	14	8	4		2			C_2v
57	prisma hexagonal triaumentado	15	30	17	12	3		2			D_3h
58	dodecaedro aumentado	21	35	16	5		11				C_5v
59	dodecaedro parabiaumentado	22	40	20	10		10				D_5d
60	dodecaedro metabiaumentado	22	40	20	10		10				C_2v
61	dodecaedro triaumentado	23	45	24	15		9				C_3v
62	icosaedro metabidiminuído	10	20	12	10		2				C_2v
63	icosaedro tridiminuído	9	15	8	5		3				C_3v
64	icosaedro tridiminuído aumentado	10	18	10	7		3				C_3v
65	tetraedro truncado aumentado	15	27	14	8	3		3			C_3v
66	cubo truncado aumentado	28	48	22	12	5			5		C_4v
67	cubo truncado biaumentado	32	60	30	16	10			4		D_4h
68	dodecaedro truncado aumentado	65	105	42	25	5	1			11	C_5v
69	dodecaedro truncado parabiaumentado	70	120	52	30	10	2			10	D_5d
70	dodecaedro truncado metabiaumentado	70	120	52	30	10	2			10	C_2v
71	dodecaedro truncado triaumentado	75	135	62	35	15	3			9	C_3v
72	girorrombicosidodecaedro	60	120	62	20	30	12				C_5v
73	parabigirorrombicosidodecaedro	60	120	62	20	30	12				D_5d
74	metabigirorrombicosidodecaedro	60	120	62	20	30	12				C_2v
75	trigirorrombicosidodecaedro	60	120	62	20	30	12				C_3v
76	rombicosidodecaedro diminuído	55	105	52	15	25	11			1	C_5v
77	rombicosidodecaedro paragirodiminuído	55	105	52	15	25	11			1	C_5v
78	rombicosidodecaedro metagirodiminuído	55	105	52	15	25	11			1	C_s
79	rombicosidodecaedro bigirodiminuído	55	105	52	15	25	11			1	C_s
80	rombicosidodecaedro parabidiminuído	50	90	42	10	20	10			2	D_5d
81	rombicosidodecaedro metabidiminuído	50	90	42	10	20	10			2	C_2v
82	rombicosidodecaedro girobidiminuído	50	90	42	10	20	10			2	C_s
83	rombicosidodecaedro tridiminuído	45	75	32	5	15	9			3	C_3v
84	disfenoide achatado	8	18	12	12						D_2d
85	antiprisma quadrado achatado	16	40	26	24	2					D_4d
86	esfenocorona	10	22	14	12	2					C_2v
87	esfenocorona aumentada	11	26	17	16	1					C_s
88	esfenomegacorona	12	28	18	16	2					C_2v
89	Hebesfenomegacorona	14	33	21	18	3					C_2v
90	disfenocingulum	16	38	24	20	4					D_2d
91	birrotunda bilunar	14	26	14	8	2	4				D_2h
92	hebesfenorrotunda triangular	18	36	20	13	3	3	1			C_3v

Referências

Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contém a enumeração original dos 92 sólidos.
Victor A. Zalgaller, "Convex Polyhedra with Regular Faces", 1969.

Ligações externas

«Modelos de papel de poliedros» (em inglês)
«Johnson Solids». por George W. Hart. (em inglês)
«Imagens dos 92 sólidos e classificações.» (em inglês)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.